-スポンサーリンク-
リアルが忙しくて全然更新できていませんね。4月からも月1で更新できれば上出来でしょう。
2024年度の北海道,数学は(記述は面倒ですが)問題自体はとても簡単でしたね。
記述が面倒なのは毎年のことなので,むしろ数学得意な子が「全然差がつかない!」と怒った入試でしたでしょう。
逆に,国語,社会,理科が厳しかったですね。
社会は......難関私立中学入試じゃないんだからと思いました。”公立”高校入試ですよ。みんながみんなSAPIXや日能研通っているわけじゃないんだから。中学校の先生は最近の入試に対してどう教えているのでしょうか?キツそう。
理科は相変わらずイカれていますね。職場の人間と話しましたが「私たちが中学生の頃より,絶対に理科は何倍も何倍も難しくなっている」「問題も難しいし,問われる知識も細かくなっている」とのことでした。理科教員は大変だ。
その割には数学は易しいですね。難しすぎて誰も解けない!みたいな入試よりはマシですが。
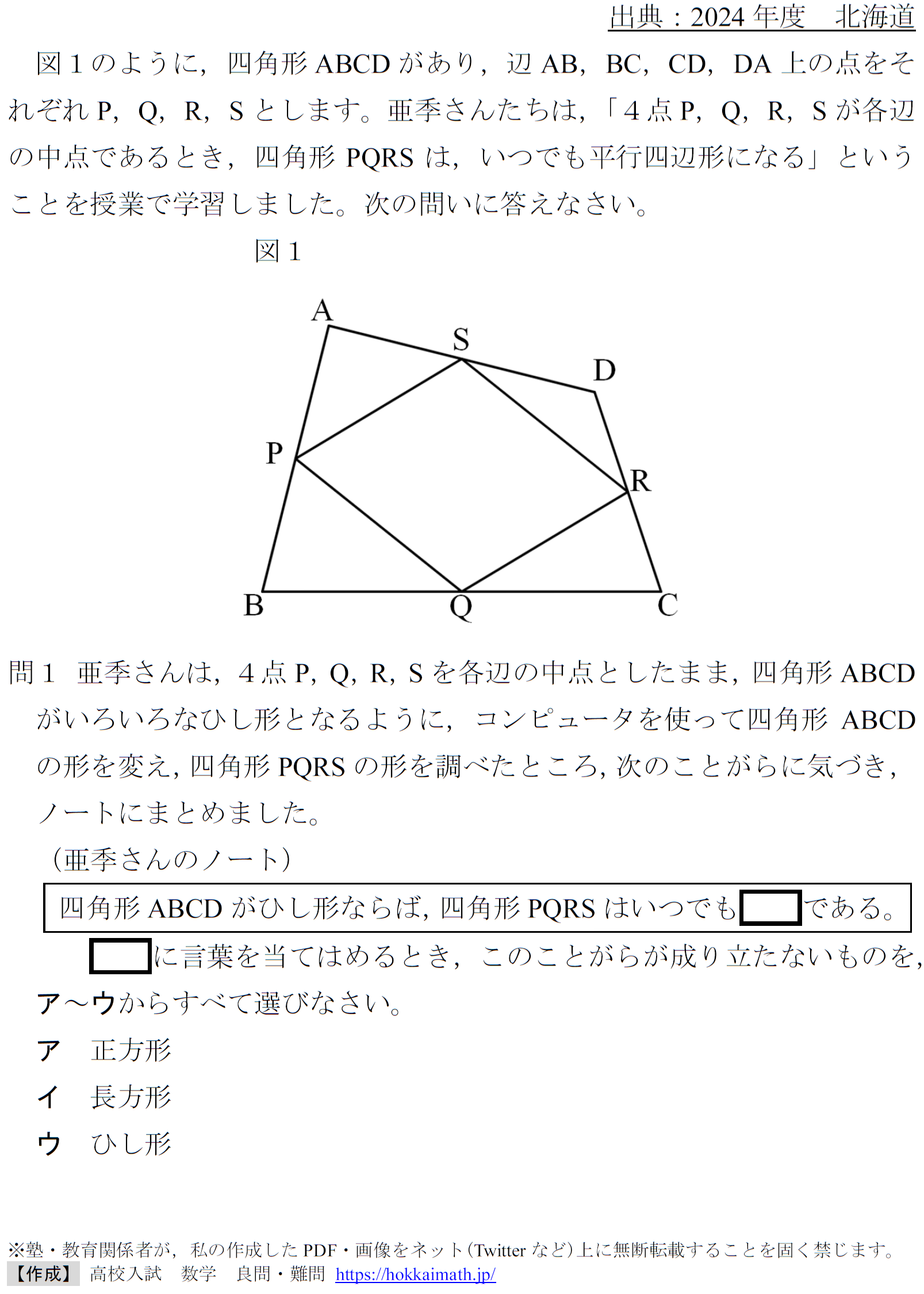
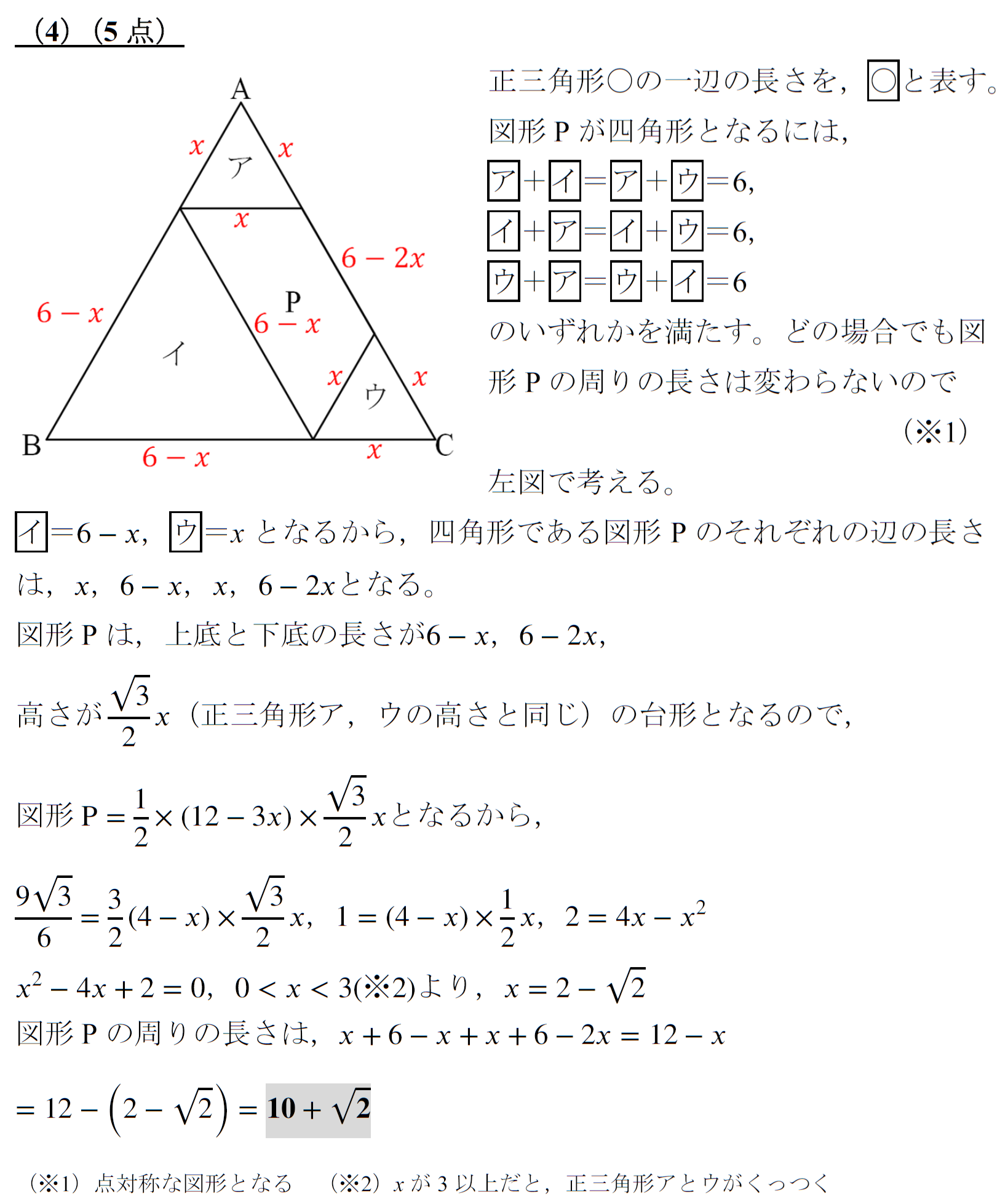
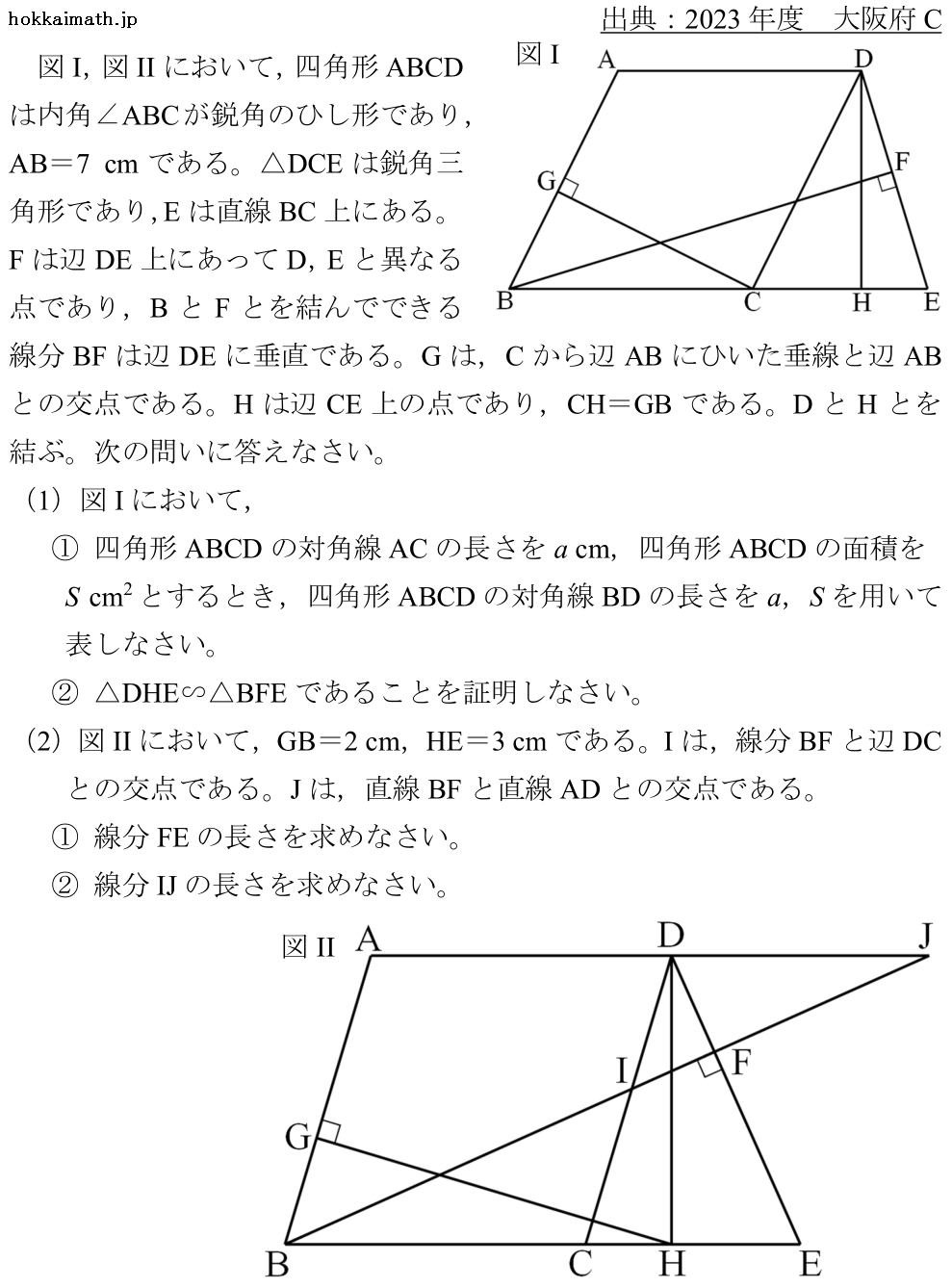
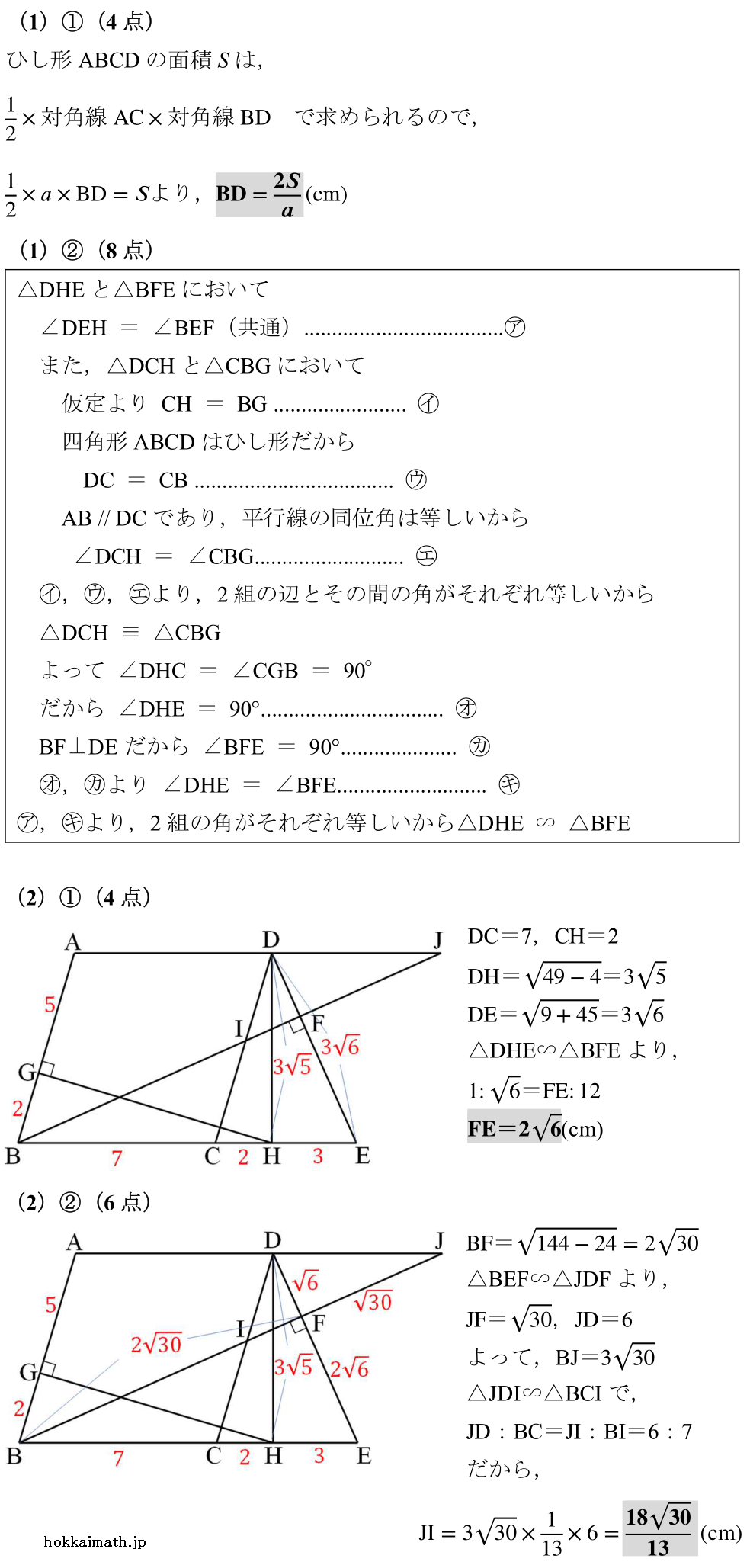
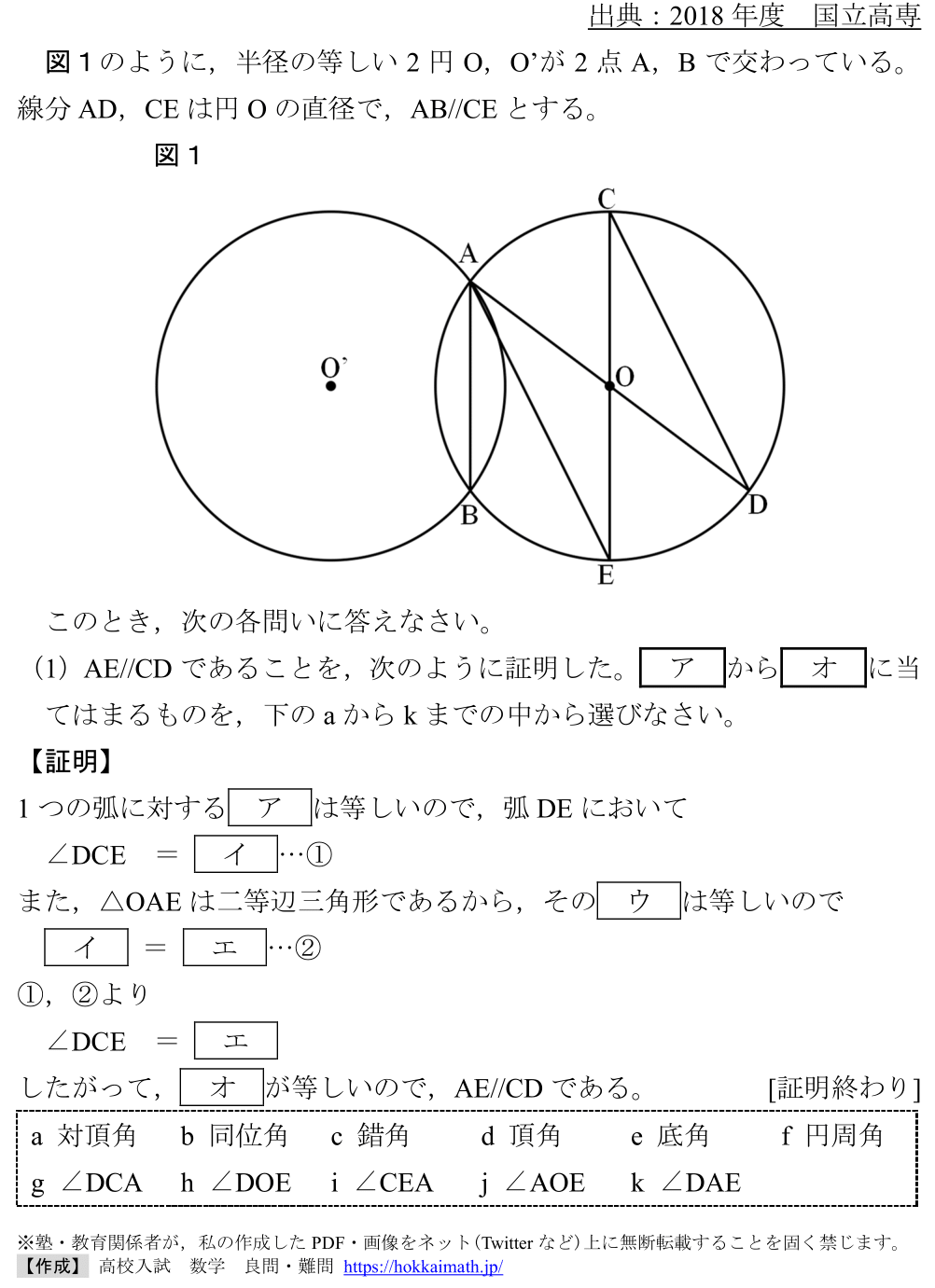
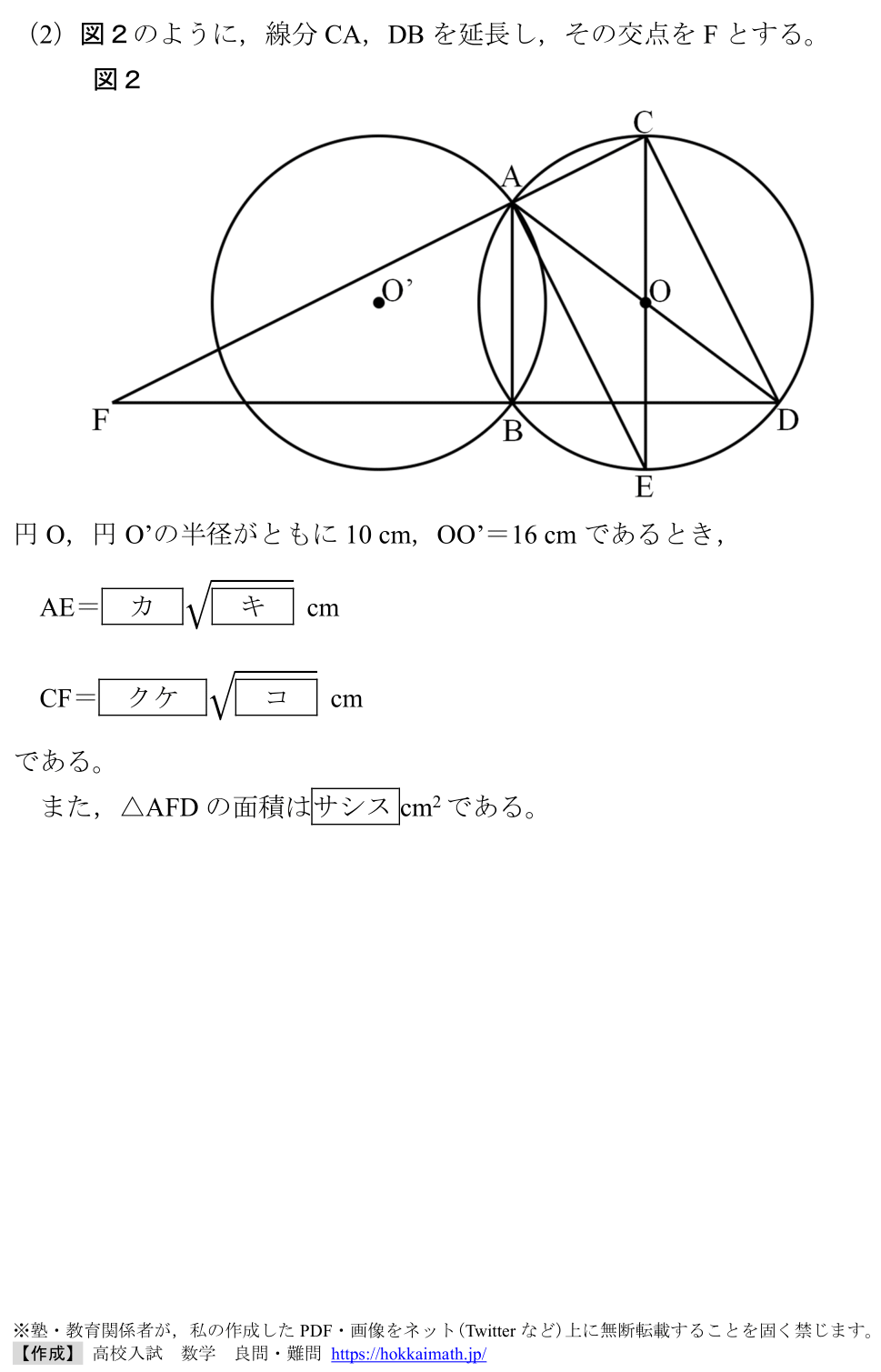
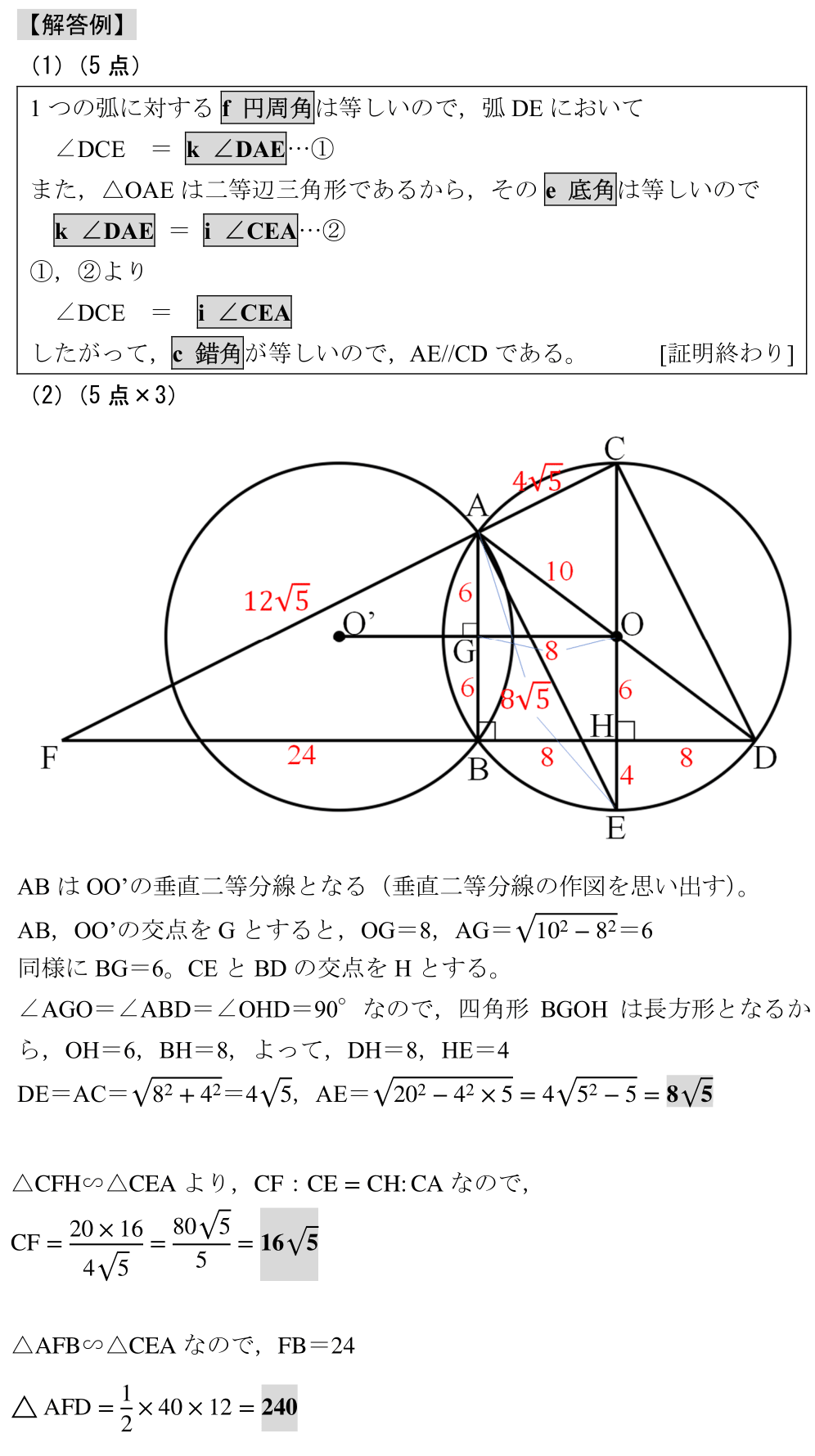
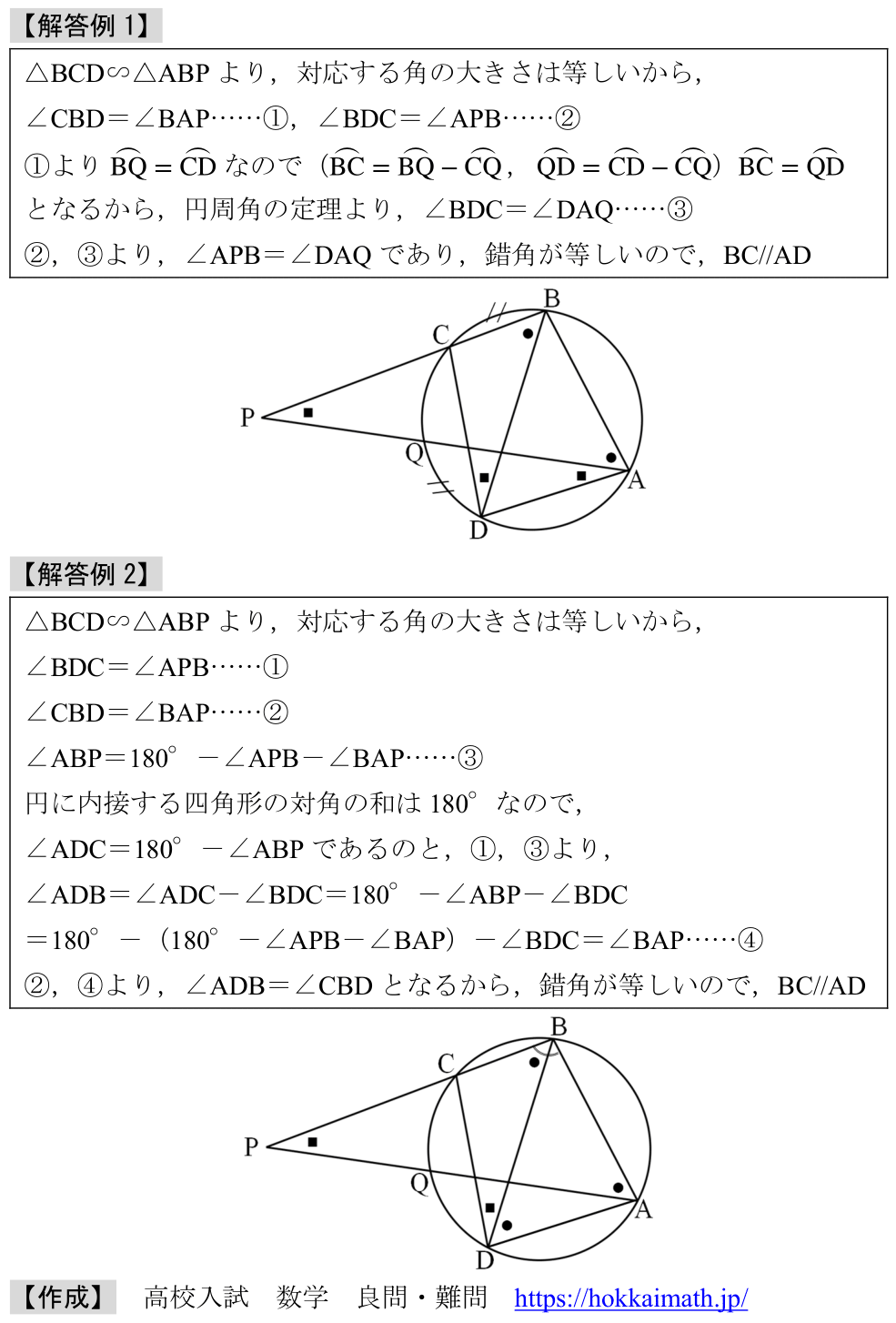
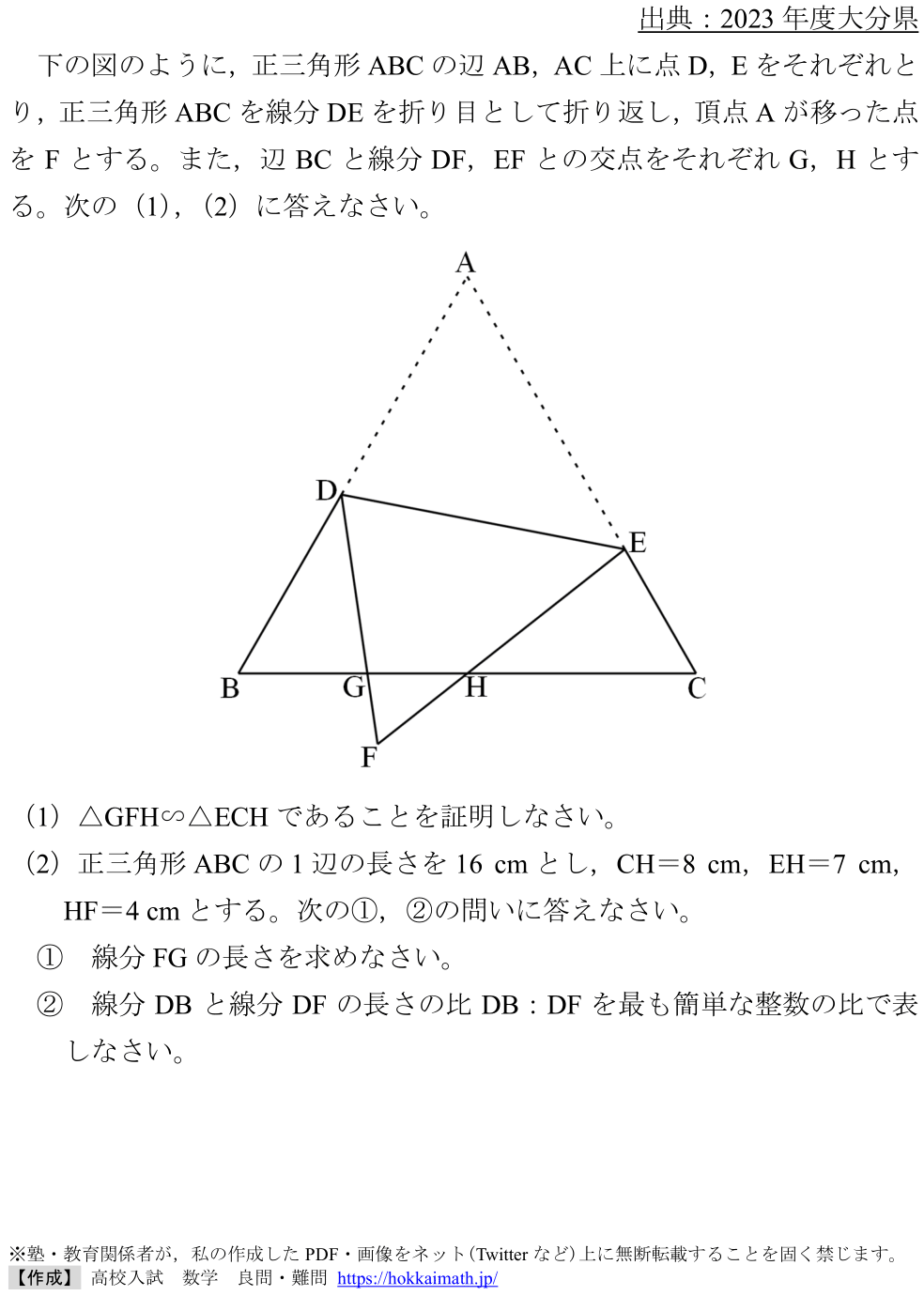
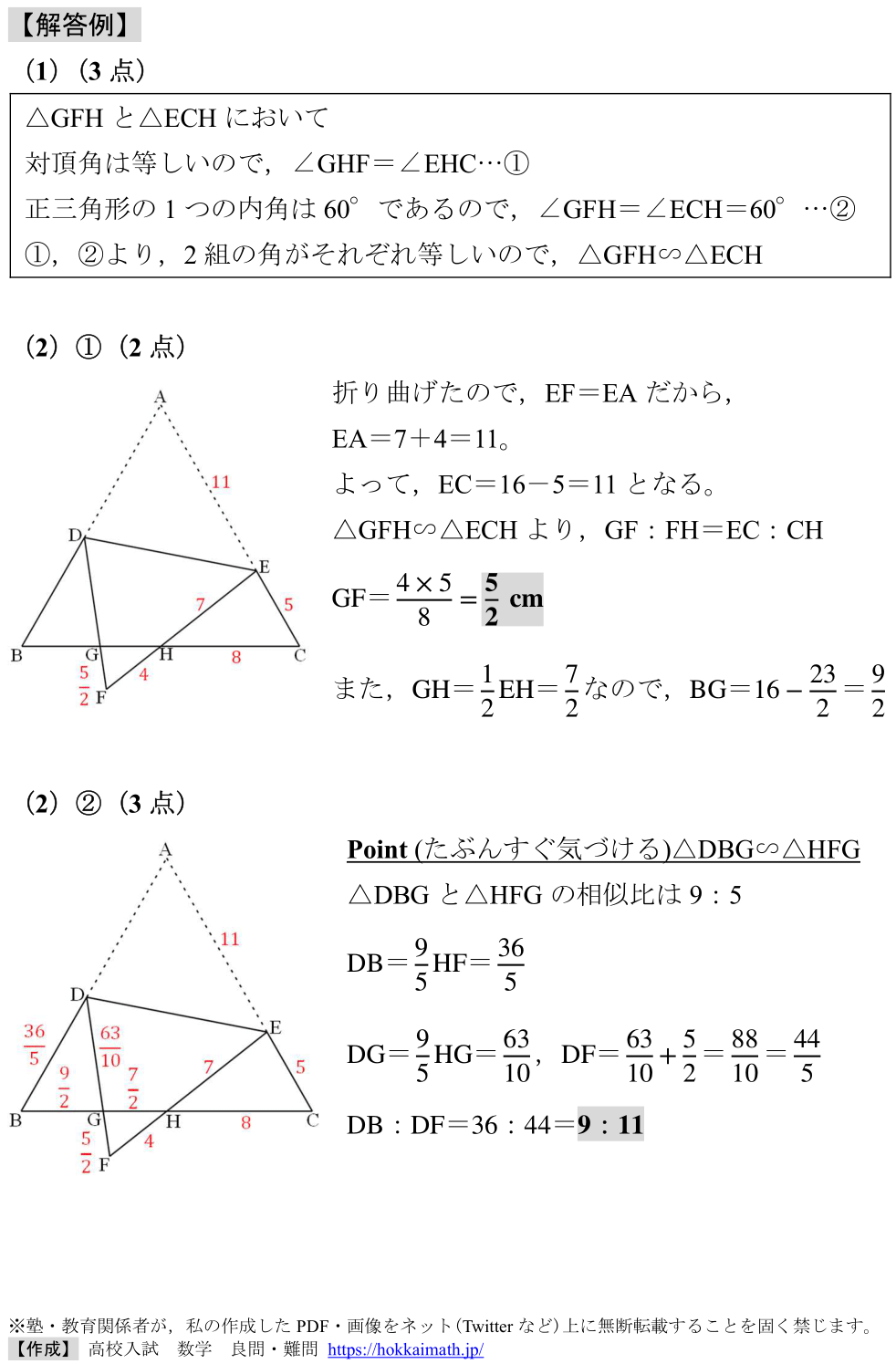
「四角形のbasic問題」
出典:2024年度 北海道
範囲:平面図形(中3),難易度:★×4
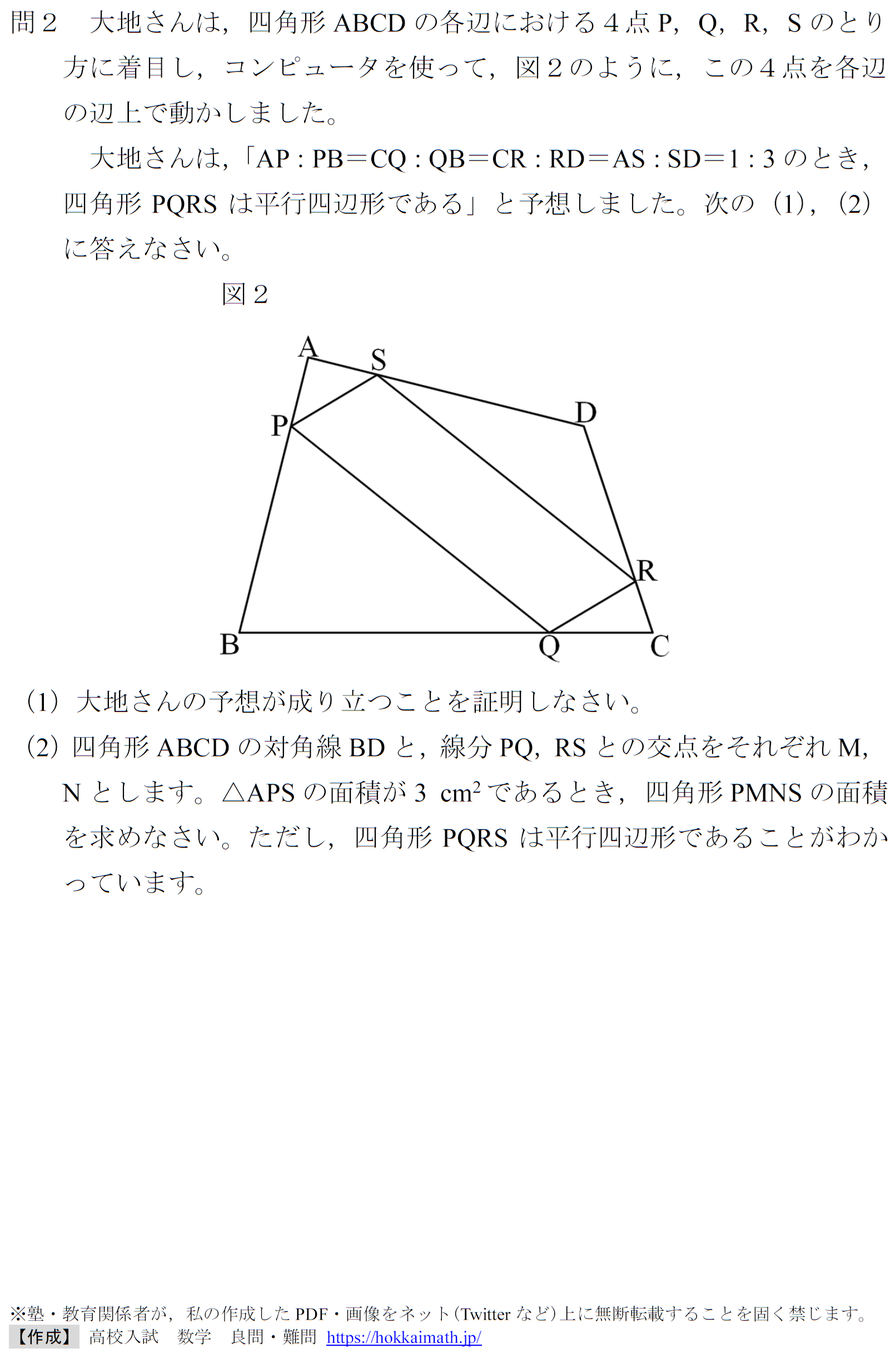
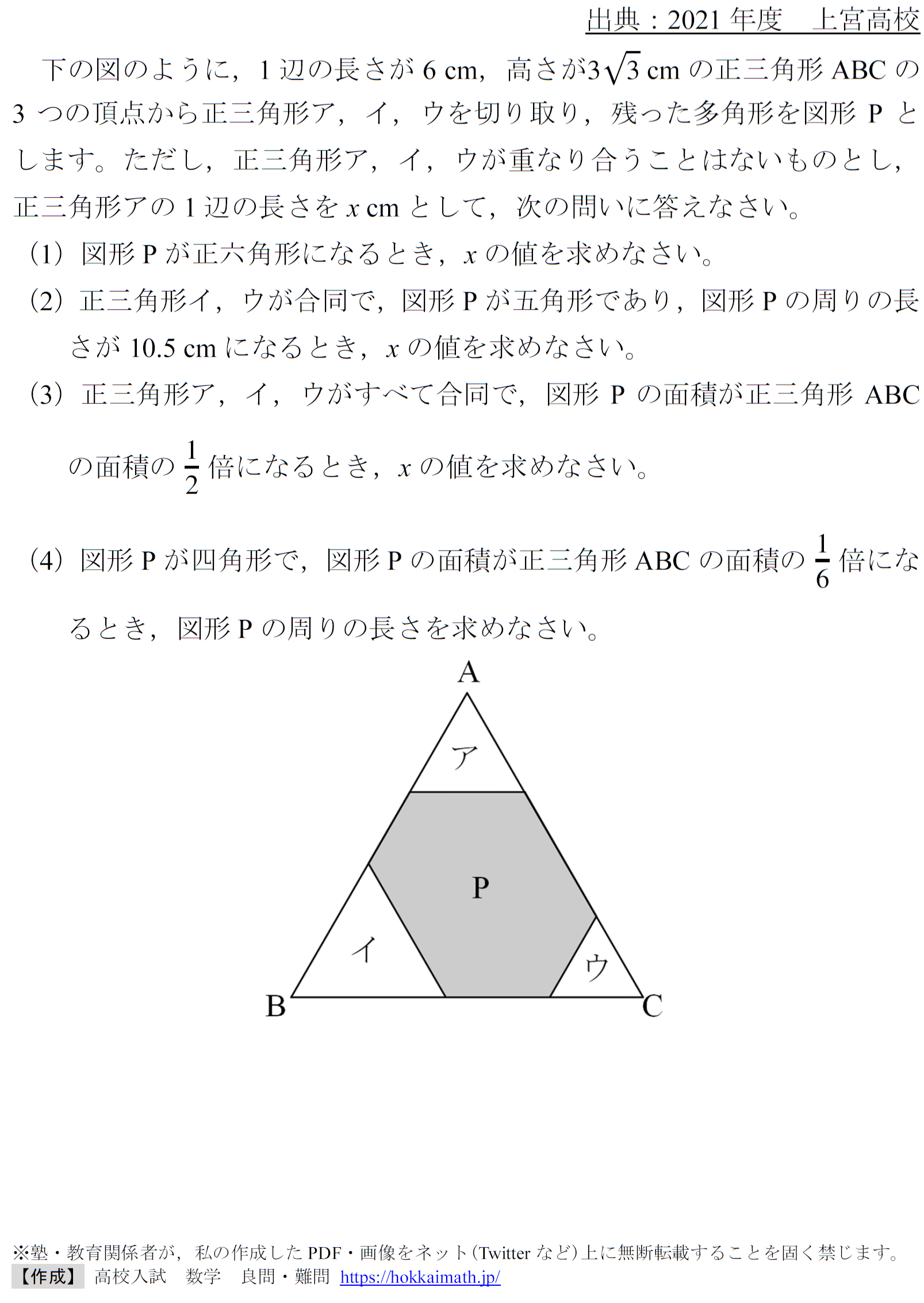
<問題>
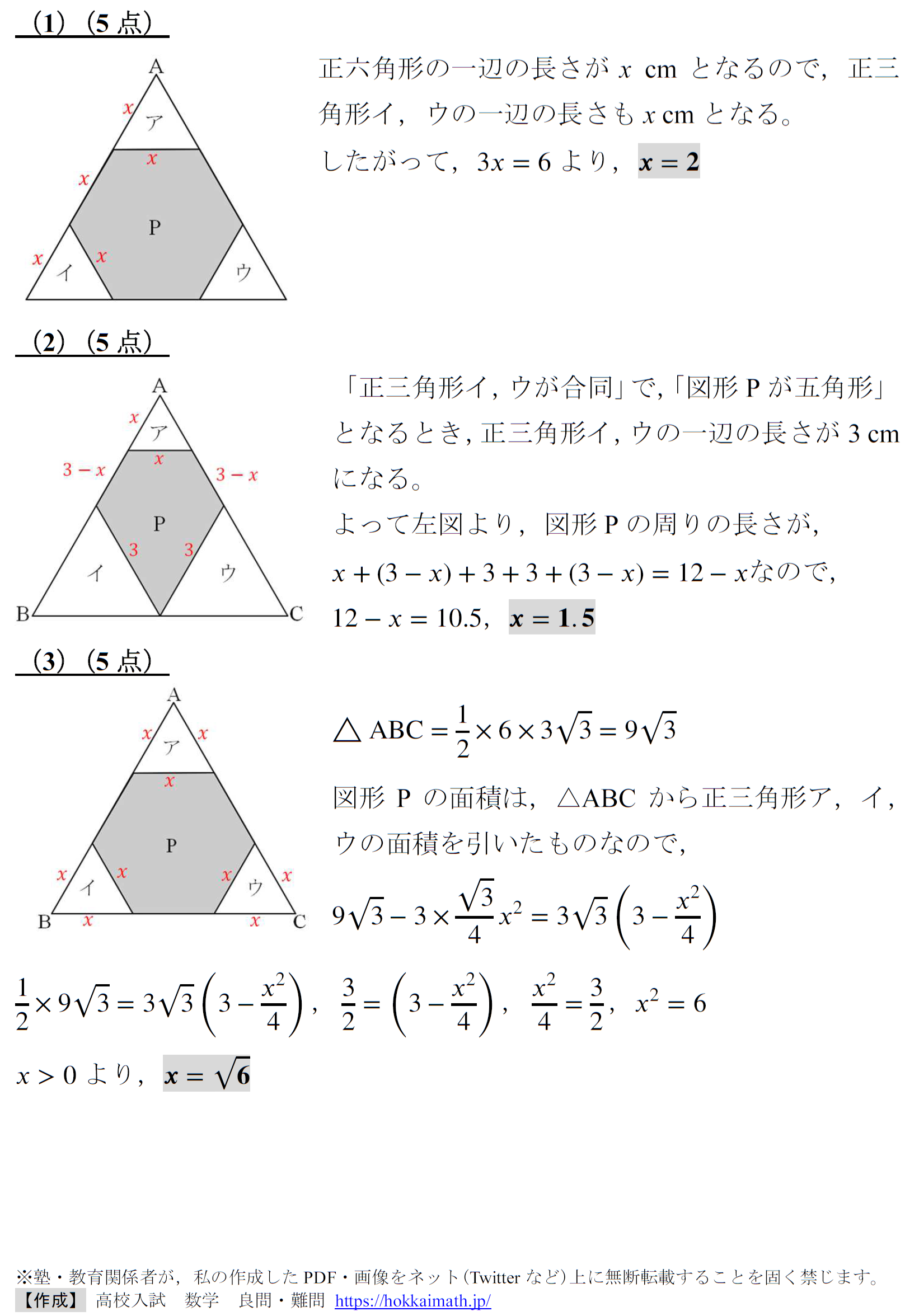
<PDF,解答例はこちら↓↓>
2024年度の北海道,数学は(記述は面倒ですが)問題自体はとても簡単でしたね。
記述が面倒なのは毎年のことなので,むしろ数学得意な子が「全然差がつかない!」と怒った入試でしたでしょう。
逆に,国語,社会,理科が厳しかったですね。
社会は......難関私立中学入試じゃないんだからと思いました。”公立”高校入試ですよ。みんながみんなSAPIXや日能研通っているわけじゃないんだから。中学校の先生は最近の入試に対してどう教えているのでしょうか?キツそう。
理科は相変わらずイカれていますね。職場の人間と話しましたが「私たちが中学生の頃より,絶対に理科は何倍も何倍も難しくなっている」「問題も難しいし,問われる知識も細かくなっている」とのことでした。理科教員は大変だ。
その割には数学は易しいですね。難しすぎて誰も解けない!みたいな入試よりはマシですが。
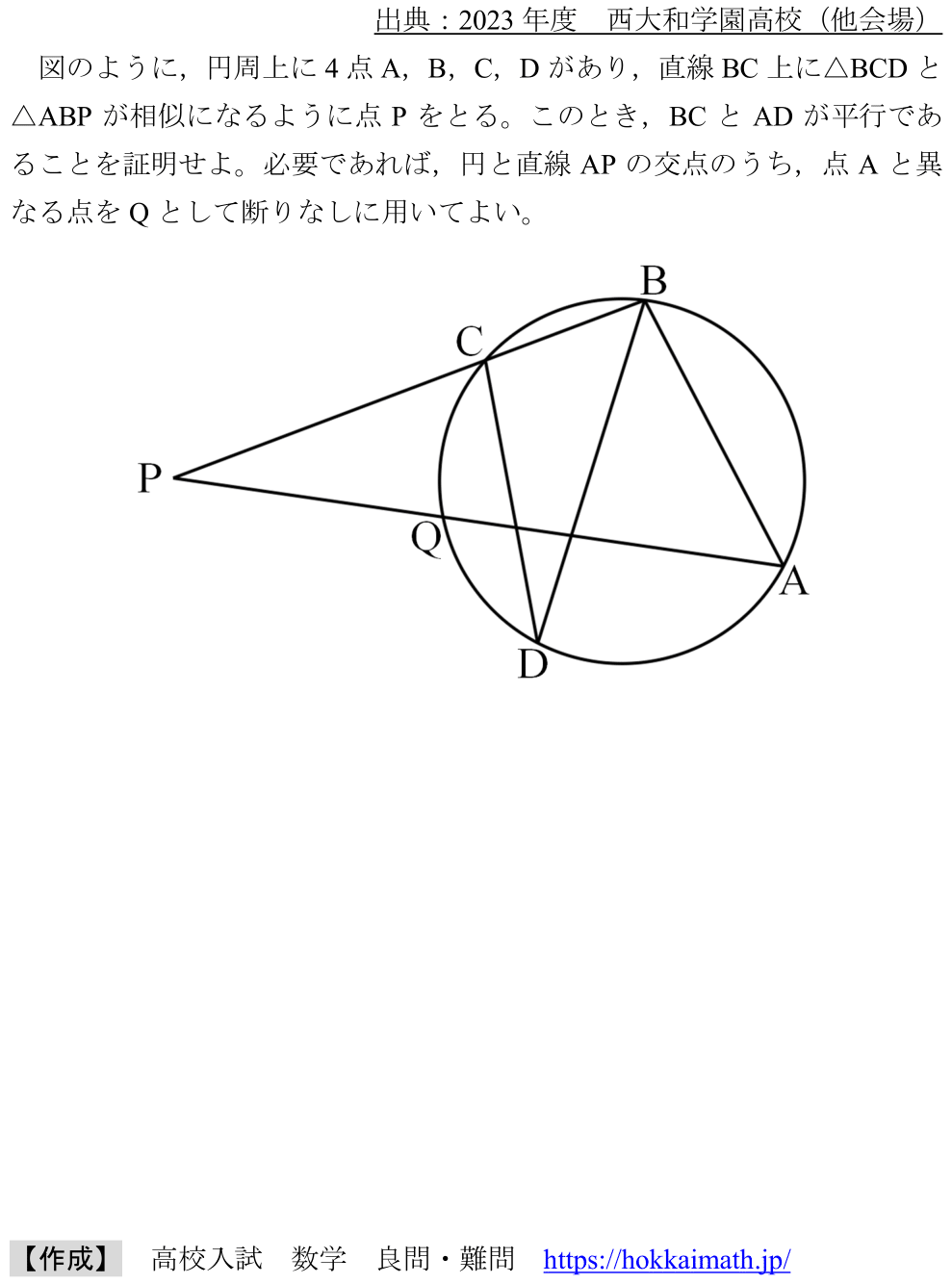
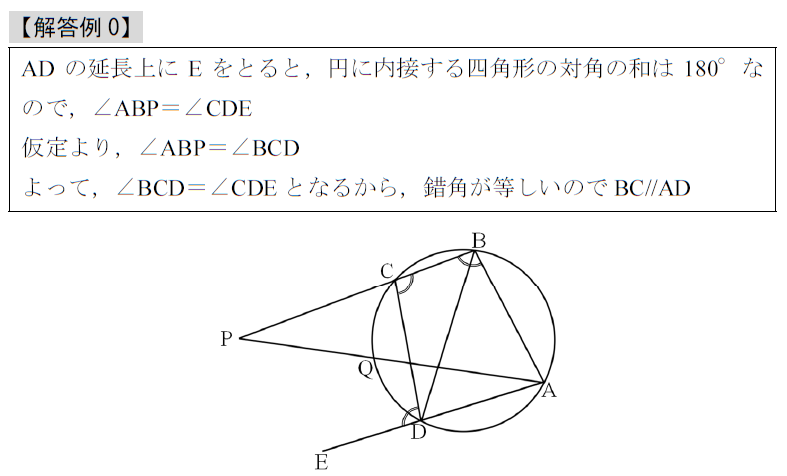
「四角形のbasic問題」
出典:2024年度 北海道
範囲:平面図形(中3),難易度:★×4
<問題>
<PDF,解答例はこちら↓↓>