-スポンサーリンク-
一覧の一覧
① ジャンル別 中学数学プリント一覧
② 良問難問入試問題(高校受験,中学数学)の一覧
③ 北海道高校入試 学校裁量問題 解説の一覧
④ 大学入試一覧
⑤ 北海道公立高校入試 数学予想問題などの一覧
① ジャンル別 中学数学プリント一覧
② 良問難問入試問題(高校受験,中学数学)の一覧
③ 北海道高校入試 学校裁量問題 解説の一覧
④ 大学入試一覧
⑤ 北海道公立高校入試 数学予想問題などの一覧
「問題集の問題に加えて,足りないものをプリントで補いたい。」
「塾の先生の指導はいらない。紙の解説だけで良い。」
「難問の高校受験の数学が解きたい!」
という方などを想定して,中学数学プリントをPDFで配布するサイトを作りました。ご自由にお使いください!受験対策にも日頃の学習にも趣味にも最適!難易度別(★×1~★×10)に整理されています!
ジャンル別に探す
日頃の学習用,入試対策用として,悪問から普通の問題,良問の区別なくまとめております。主に入試問題ですが,中には定期テスト対策に役立つものもあります!プリント利用は,お好きにどうぞ。全て解答・解説付きです。
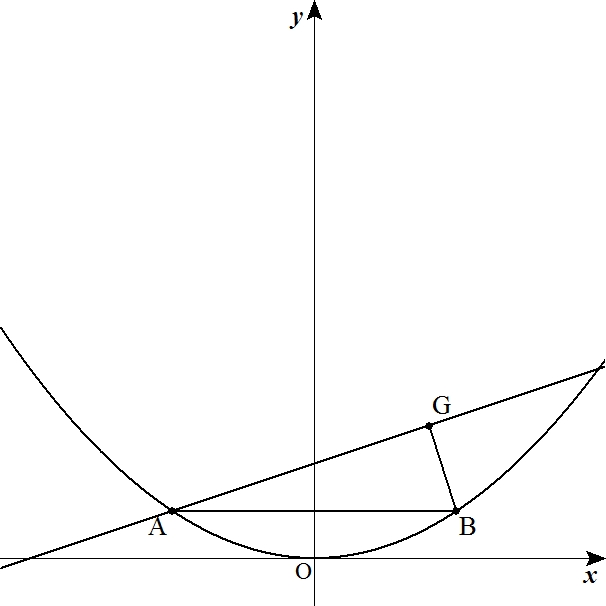
・関数 プリント一覧
北海道では配点の1/6以上は出てしまう関数分野です(酷いときは約1/3!)捨てるなんてとんでもない!
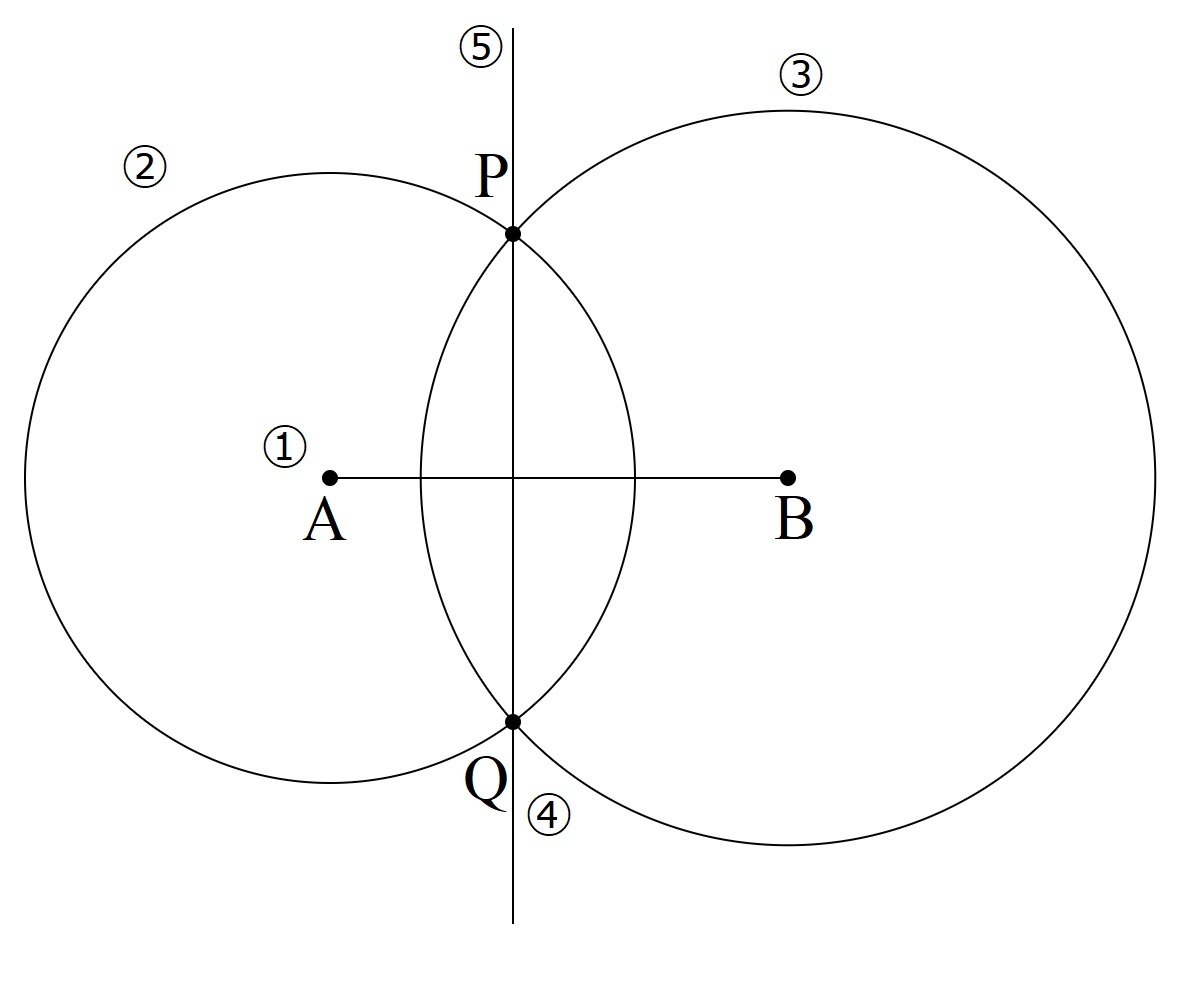
・証明,平面図形 プリント一覧
入試でよくでる証明問題をまとめてあります。
他にも,計算が難しい平面図形の問題も多数用意。Youtubeとかで再生回数稼ぎやすいのは平面図形の問題。
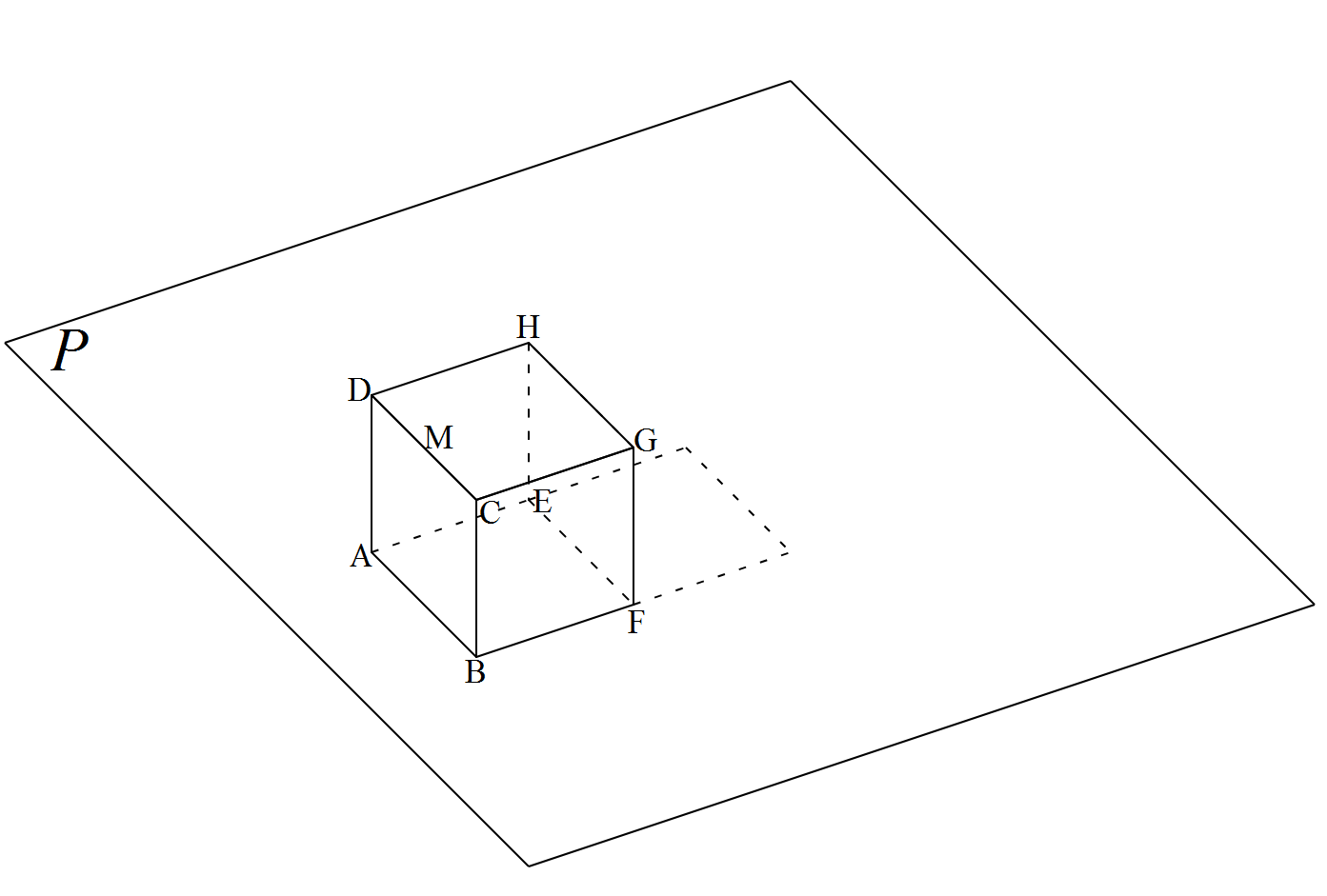
・空間図形 プリント一覧
かなり難しい問題。中1分野から難しい......。問題作るのも大変。
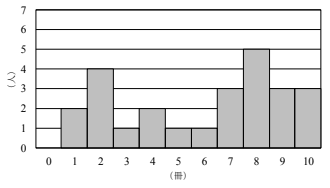
・その他の問題 プリント一覧
小問集合,方程式,資料の整理,確率,整数問題......など,上記以外の雑多な問題はここに分類してます。
最近資料の整理のごり押し激しい。
良問・難問を探す
良問難問一覧
良問な高校入試の問題を,様々な面から突っ込みます。「図がシンプルだけど難問」な入試問題や「面白い問題」「色々知れる問題」を集めています。おまけとして,悪問(?)も紹介しております。
難問(★×5以上)一覧
当ブログの難問を,ジャンル,良問悪問の区別なしにまとめてあります。
北海道 裁量問題
北海道高校入試 数学 裁量問題 解説裁量問題(北海道高校入試における,すげえ難しい問題のこと)の詳しい解説を載せています。問題集の解答を読んでもわからなかったときに,最終手段としてお使いください。平成21年度を除き,正答率がついているので,難易度の参考にもなります。
大学入試
・大学入試用 数学プリント
おまけです。
北海道高校受験 数学予想問題シリーズ
北海道の公立高校入試対策のために作成した,数学予想問題集です。ちょっと偏った問題多い気もしますが,何かの役に立つかもしれません。全体的に難しめです。・平成30年度 予想問題
しかし問題はほとんど的中せず(当たり前だが)。大問2と似た問題が平成31年度に出ると言う。
・平成31年度 予想問題1
かなり難しい。と思っていたけどそうでもないですね。
・平成31年度 予想問題3
トリッキーな問題が多いです。
・令和2年度 予想問題1
わざと難易度上げています。
・令和3年度 予想問題1
相似以降カットでも案外何とかなるもんだ!
・令和3年度 予想問題2
相似以降カットでも案外何とかなるもんだ!(2)
新入試対応,50分の使い方に慣れよう。本番どんな問題出るんでしょうね。
大問2で北海道の気候変動の話していますが,令和4年度ではなく令和5年度で出ました。残念!
・令和5年度 予想問題
令和4年度が思ったより難しかったのですが,令和5年度は思ったよりかなり簡単でした。残念。
・令和6年度 予想問題
イライラしてて,若干見たことねぇよ!と言いたくなる問題増やしてみました。