-スポンサーリンク-
<PDF>※A5サイズです,2in1がおすすめ
kuruma2.pdf
<解答解説>
<コメント>
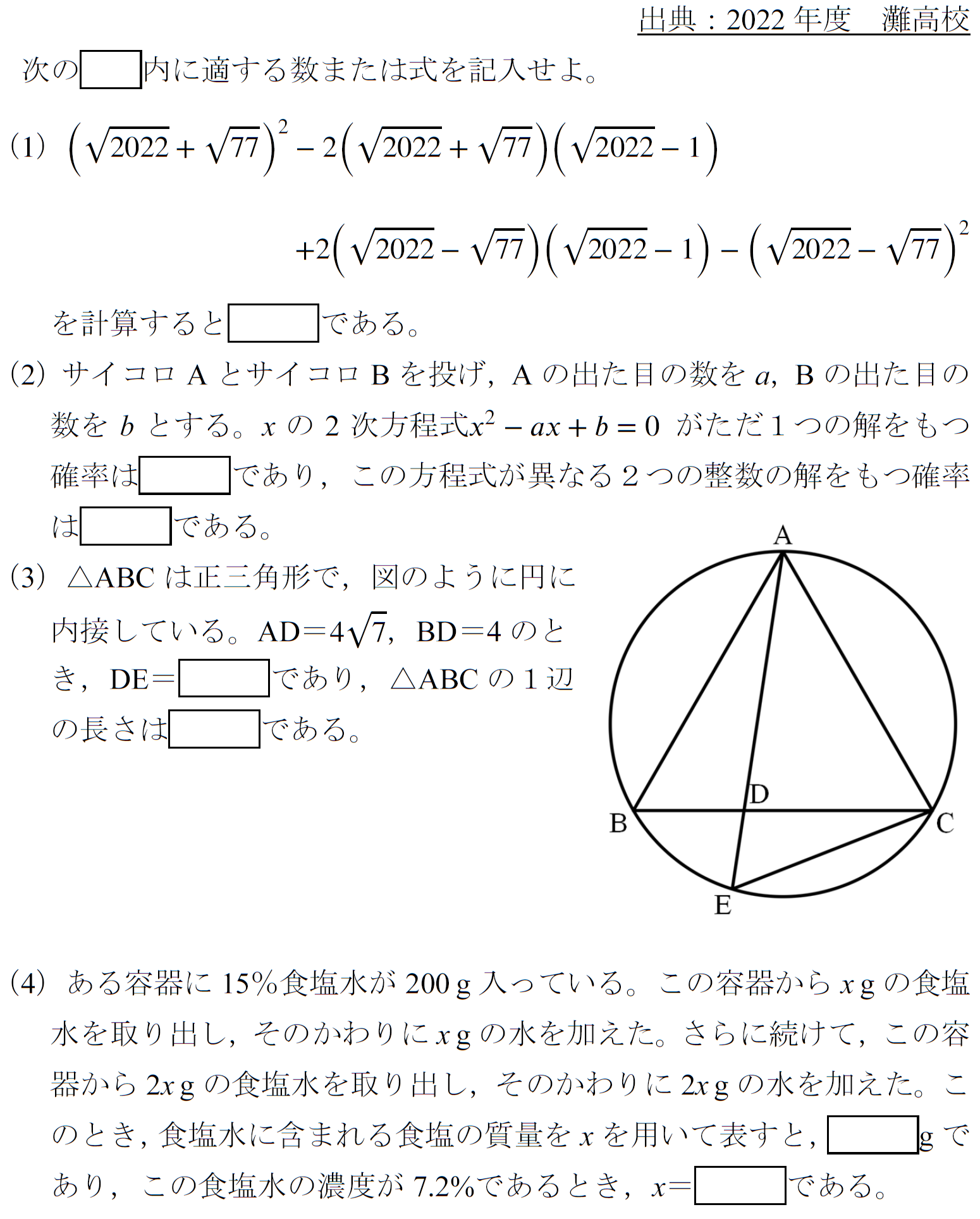
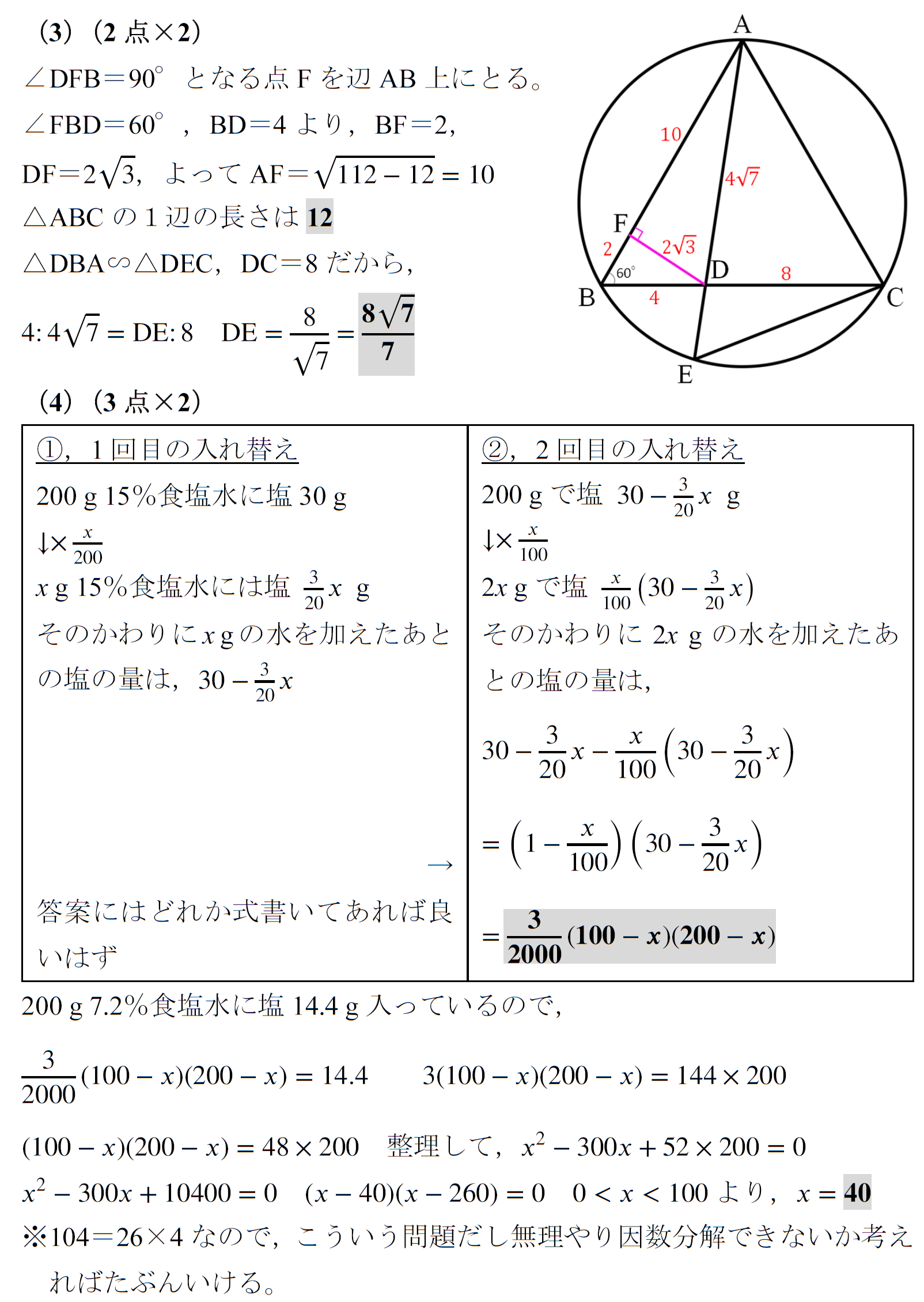
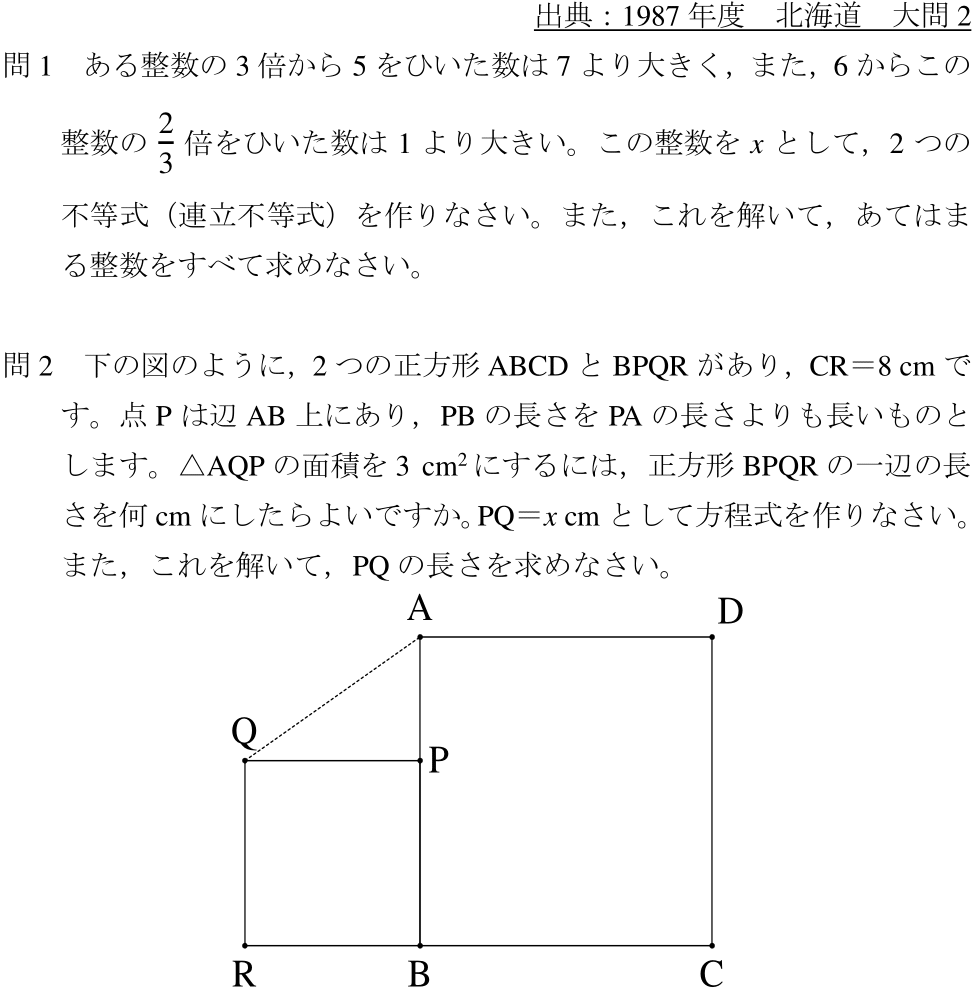
395=79×5と気づき,3239が79で割れるか試してみる問題です。一般的な人は気づくのでしょうか。連立方程式の立式は定期テストレベルですが,数字の大きさで嫌になる子多そうです。
<余談1>今年の人気記事 2023/1/1~2023/12/30
GA4の扱い方が難しいのですが,今年のPV(SV)は629123回でした。ほとんど更新してなかったのに,お越しいただける方,本用にありがとうございます。
一覧系・TOPページ記事を除くと,人気記事は次のようになりました。
①,激ヤバ計算小問集合(2023年度灘高校) 14735 PV
https://hokkaimath.jp/blog-entry-386.html
②,【正答率1.2%】謎な男女の連立方程式文章題難問(1981年沖縄県)(別解たくさん) 8433PV
https://hokkaimath.jp/blog-entry-235.html
③,激ムズ食塩水(2022年度灘) 7040PV
https://hokkaimath.jp/blog-entry-317.html
④,【正答率0.1%】どうあがいても絶望(2018大分県) 5034PV
https://hokkaimath.jp/blog-entry-177.html
⑤,一瞬手が止まる方程式文章題(2012年度栃木県) 4202PV
https://hokkaimath.jp/blog-entry-313.html
小問集合や文章題が人気みたいですね。
空間図形は労力の割にPV稼ぎません。
灘の小問集合だけでも更新しておきますか。ネームバリューすげぇ。
<余談2>M-1 2023 感想
リアルタイムで採点しながら楽しんでいました(LINEで友達にリアルタイム送信していました,私嫌な奴)。
採点言っても,好み,その場のノリに全振りですが。
カゲヤマさんが点数付けても良いおっしゃってたので,この楽しみはやめません。
■敗者復活戦
今年からルール変わって良かったか悪かったかは分かりませんが,出場者には納得しやすい......分,言い訳しづらくなって余計辛いかもしれません。
【Aブロック】
華山 84点
ぎょうぶ 86点
ロングコートダディ 91点
ニッポンの社長 88点
20世紀 98点
ママタルト 96点
ヘンダーソン 99点
【Bブロック】
豪快キャプテン 85点
鬼としみちゃむ 90点
スタミナパン 97点
トム・ブラウン 96点
エバース 93点
ナイチンゲールダンス 92点
オズワルド 89点
【Cブロック】
ドーナツ・ピーナツ 83点
きしたかの 87点
シシガシラ 96点
ダイタク 92点
ななまがり 93点
バッテリィズ 100点
フースーヤ 95点
ブロック後半の方が点数高いので,やはり順番の有利不利あるかもしれませんね。
(準決勝の順位が上の方が順番後半だったらしいですが)。
個人的にはバッテリィズが一番面白かったです。多くの道産子は100点つけているかもしれません。
■決勝1st
①,令和ロマン 93点
これはね,今年の審査員偉かったですね。ちゃんと令和ロマンの基準を忘れていませんでしたね。
私はトップバッターだからと鬼厳しく93点つけてしまいましたが,後から考えたら96点で良かった気がします。
本当面白かった。
②,シシガシラ 91点
同じネタやらなかったの格好良すぎますね。
③,さや香 97点
流石の安定感。
④,カベポスター 94点
昨年と違うのは,永見さんが本当にやってそうな,脳内で想像しやすかったところですね。
大声大会はフィクションなのかノンフィクションなのか曖昧でした(もちろんフィクションなのですが,リアルさが微妙だと脳内が混乱する)。
⑤,マユリカ 92点
私不倫や仲悪いカップルネタが好きじゃないので,こんな低い点数となりました。こればかりは好み。
ちょっと生々しかった。
⑥,ヤーレンズ 98点
楢原さんのフアンです。
⑦,真空ジェシカ 97点
最初「?」となりましたが,後半の追い上げとカオスさは流石ですね。
何でクニちゃん点数低かったんだろ,老人出さなかったからだろうか,不思議。
⑧,ダンビラムーチョ 90点
先鋭的すぎて難しかった......。
⑨,くらげ 91点
面白いけど変化欲しかった。
⑩,モグライダー 96点
これは甘く付けました。でも好きだなー。練習不足というよりは,練習しすぎ,慣れすぎた?
■決勝ファイナル
①,令和ロマン 97点
トヨタと吉本でやられました。
②,ヤーレンズ 99点
昨年の敗者復活をややアレンジしたネタですね。でも昨年より良くなっていました。
もうやめてくれー,爆笑が止まりませんでした。
③,さや香 89点
ネタは面白いのですが,個人的には教育学部を思い出してしまって辛かった。
令和ロマンさん,おめでとう!
若くてプレッシャーでしょうが,負けずに楽しんでほしいです。確実に一番面白いので。
..end
kuruma2.pdf
<解答解説>
<コメント>
395=79×5と気づき,3239が79で割れるか試してみる問題です。一般的な人は気づくのでしょうか。連立方程式の立式は定期テストレベルですが,数字の大きさで嫌になる子多そうです。
<余談1>今年の人気記事 2023/1/1~2023/12/30
GA4の扱い方が難しいのですが,今年のPV(SV)は629123回でした。ほとんど更新してなかったのに,お越しいただける方,本用にありがとうございます。
一覧系・TOPページ記事を除くと,人気記事は次のようになりました。
①,激ヤバ計算小問集合(2023年度灘高校) 14735 PV
https://hokkaimath.jp/blog-entry-386.html
②,【正答率1.2%】謎な男女の連立方程式文章題難問(1981年沖縄県)(別解たくさん) 8433PV
https://hokkaimath.jp/blog-entry-235.html
③,激ムズ食塩水(2022年度灘) 7040PV
https://hokkaimath.jp/blog-entry-317.html
④,【正答率0.1%】どうあがいても絶望(2018大分県) 5034PV
https://hokkaimath.jp/blog-entry-177.html
⑤,一瞬手が止まる方程式文章題(2012年度栃木県) 4202PV
https://hokkaimath.jp/blog-entry-313.html
小問集合や文章題が人気みたいですね。
空間図形は労力の割にPV稼ぎません。
灘の小問集合だけでも更新しておきますか。ネームバリューすげぇ。
<余談2>M-1 2023 感想
リアルタイムで採点しながら楽しんでいました(LINEで友達にリアルタイム送信していました,私嫌な奴)。
採点言っても,好み,その場のノリに全振りですが。
カゲヤマさんが点数付けても良いおっしゃってたので,この楽しみはやめません。
■敗者復活戦
今年からルール変わって良かったか悪かったかは分かりませんが,出場者には納得しやすい......分,言い訳しづらくなって余計辛いかもしれません。
【Aブロック】
華山 84点
ぎょうぶ 86点
ロングコートダディ 91点
ニッポンの社長 88点
20世紀 98点
ママタルト 96点
ヘンダーソン 99点
【Bブロック】
豪快キャプテン 85点
鬼としみちゃむ 90点
スタミナパン 97点
トム・ブラウン 96点
エバース 93点
ナイチンゲールダンス 92点
オズワルド 89点
【Cブロック】
ドーナツ・ピーナツ 83点
きしたかの 87点
シシガシラ 96点
ダイタク 92点
ななまがり 93点
バッテリィズ 100点
フースーヤ 95点
ブロック後半の方が点数高いので,やはり順番の有利不利あるかもしれませんね。
(準決勝の順位が上の方が順番後半だったらしいですが)。
個人的にはバッテリィズが一番面白かったです。多くの道産子は100点つけているかもしれません。
■決勝1st
①,令和ロマン 93点
これはね,今年の審査員偉かったですね。ちゃんと令和ロマンの基準を忘れていませんでしたね。
私はトップバッターだからと鬼厳しく93点つけてしまいましたが,後から考えたら96点で良かった気がします。
本当面白かった。
②,シシガシラ 91点
同じネタやらなかったの格好良すぎますね。
③,さや香 97点
流石の安定感。
④,カベポスター 94点
昨年と違うのは,永見さんが本当にやってそうな,脳内で想像しやすかったところですね。
大声大会はフィクションなのかノンフィクションなのか曖昧でした(もちろんフィクションなのですが,リアルさが微妙だと脳内が混乱する)。
⑤,マユリカ 92点
私不倫や仲悪いカップルネタが好きじゃないので,こんな低い点数となりました。こればかりは好み。
ちょっと生々しかった。
⑥,ヤーレンズ 98点
楢原さんのフアンです。
⑦,真空ジェシカ 97点
最初「?」となりましたが,後半の追い上げとカオスさは流石ですね。
何でクニちゃん点数低かったんだろ,老人出さなかったからだろうか,不思議。
⑧,ダンビラムーチョ 90点
先鋭的すぎて難しかった......。
⑨,くらげ 91点
面白いけど変化欲しかった。
⑩,モグライダー 96点
これは甘く付けました。でも好きだなー。練習不足というよりは,練習しすぎ,慣れすぎた?
■決勝ファイナル
①,令和ロマン 97点
トヨタと吉本でやられました。
②,ヤーレンズ 99点
昨年の敗者復活をややアレンジしたネタですね。でも昨年より良くなっていました。
もうやめてくれー,爆笑が止まりませんでした。
③,さや香 89点
ネタは面白いのですが,個人的には教育学部を思い出してしまって辛かった。
令和ロマンさん,おめでとう!
若くてプレッシャーでしょうが,負けずに楽しんでほしいです。確実に一番面白いので。