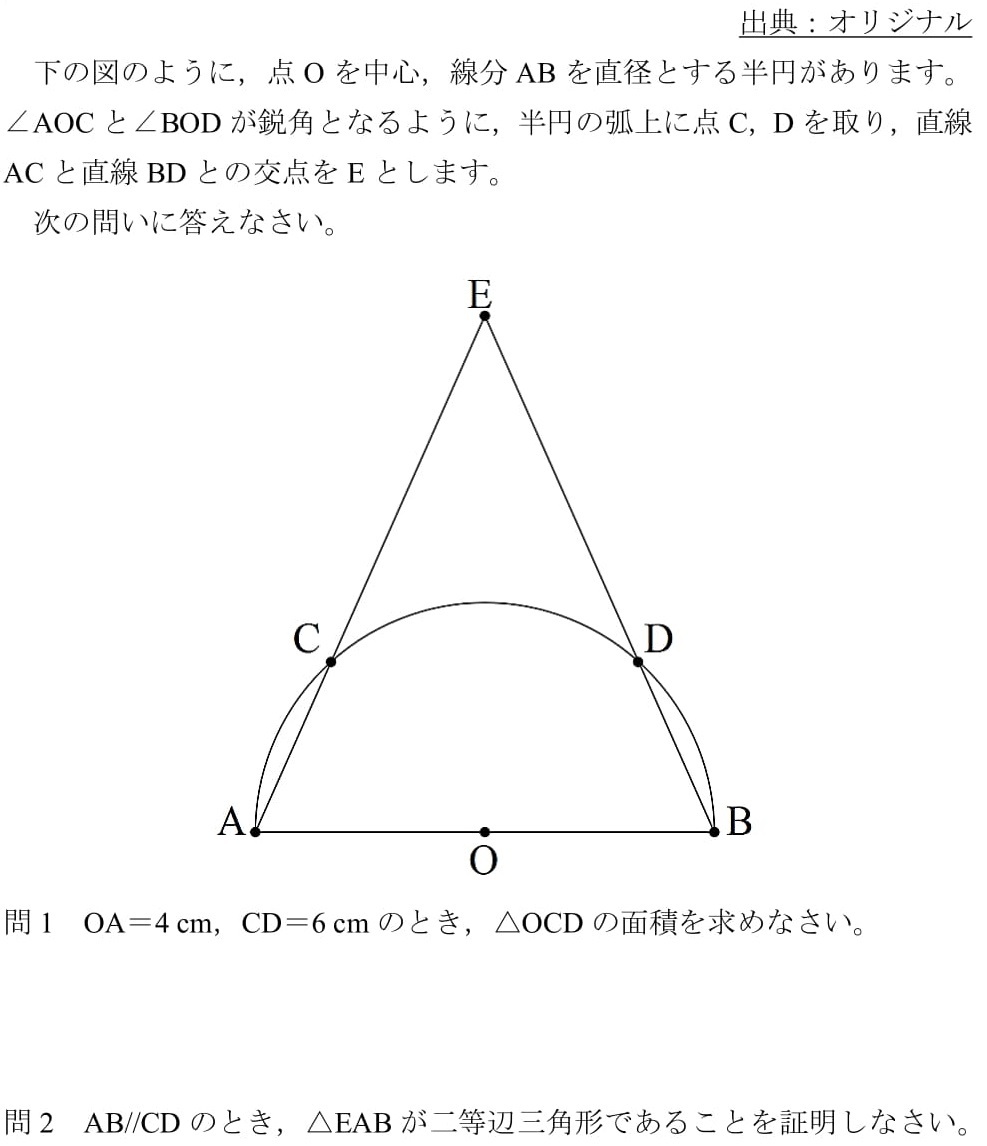
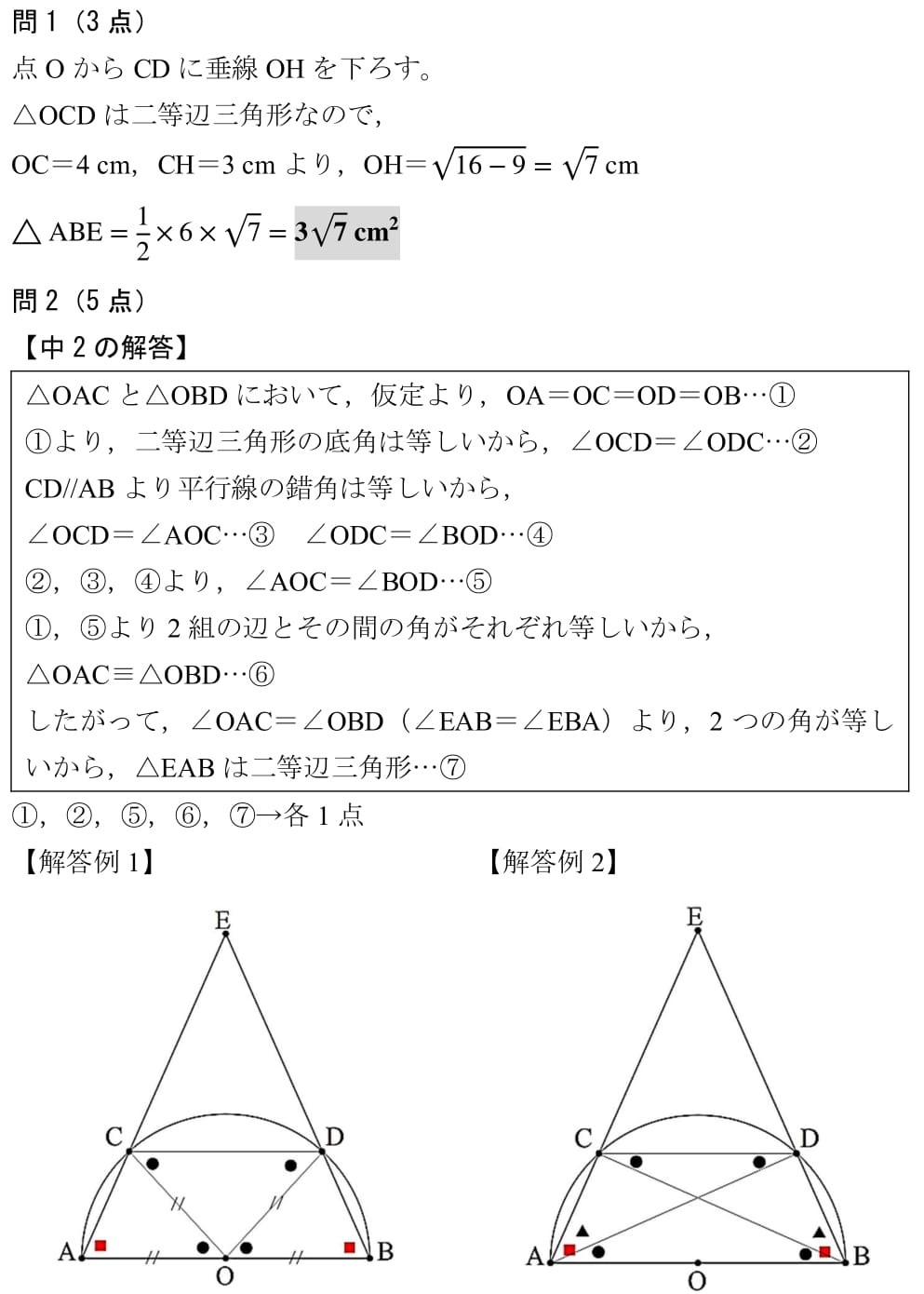
<PDF>※A5サイズです・Seesaa<解答例><コメント>問1…よくある問題です。
で,問2です。
【解答例1】は,円周角を習っていない中2でも解ける解法です。
【解答例2】は,私は思いつきませんでしたが,円周角が使える中3にぴったりの解法です。
【解答例3】はメールフォームでお問合せ頂いた解答です。最も一般的です。恐らく,このブログに来た人は,私の解答例を見て「何てまどろっこしい」と思ったでしょう。
ただ,以下の理由により,中学生に教えるのは勇気がいります。
①,都道府県によって証明の採点基準が異なる
北海道は大丈夫ですが,
例えば長野県などは「OAは円の半径なので」「長方形の全ての角は等しいから」など,普通「仮定より」で済ませていいはずの理由を,わざわざ書かないと減点されます。(定義だから省いてよくね?)
だから,県によっては,解答例の
(∠EAB=ECD,∠EBA=∠EDC
∠ACD=180°-∠ECD,∠BDC=180°-∠EDCであるから,)
を書かないと,減点されます。(北海道は減点されません)
そうすると,証明が長くなります。少しだるい。
②,円に内接する四角形の対角の和は180°は実は数A(高校範囲)中学校でも当たり前に教えていると思いますが,実は高校範囲です。中学校では「発展内容」で扱います。
そのため,中学生が断りなしに証明で使ってよいかは不明。
もしかしたら「対角の和が180°」である証明を書かないと減点されるかも?(中学範囲でも証明は容易に可能)
でもそんなことしたら,滅茶苦茶解答が長くなります。
まあ,高校の先生はそんなこと気にせず,上手く採点してくれると思いますが,長野のように採点基準がガチガチの場合,減点されます。
なお,上記の証明で
「円に内接する台形は,必ず等脚台形」ということが分かります。
ということで,このブログでは「高校入試対策」が昔は目的だったので,【解答例3】は載せておりませんでしたが,メールフォームでお問合せ頂いたので,載せました。
たぶんこの問題,自分で作りましたが,このように採点基準が非常に面倒なことになるので,入試では出ません!!