2019年07月高校入試　数学　良問・難問

2等分線と垂直からアレ（2010年度：ラ・サール高校）ベクトル禁止？

2019/07/28

-スポンサーリンク-

PDFなどは続きからをクリックよろしくお願いします。

芸術的な高校入試第7回
出典：2010年度　鹿児島ラサール（高校）
難易度：★★★★★☆ 美しさ：★★★★☆☆
総試験時間：90分配点：7点/100点？

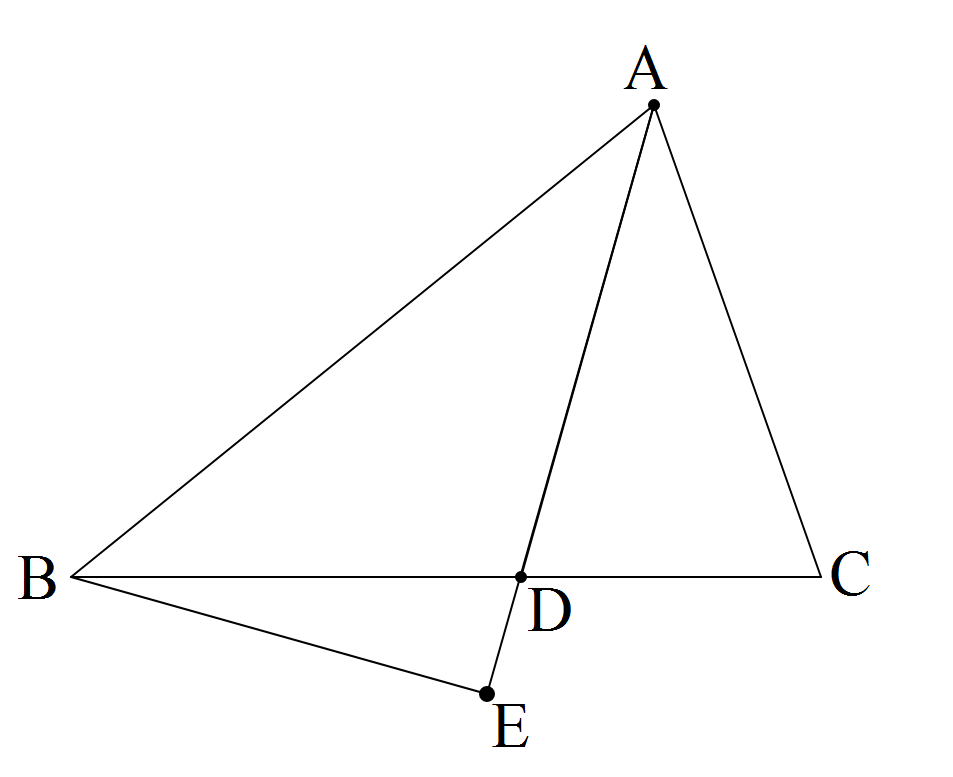
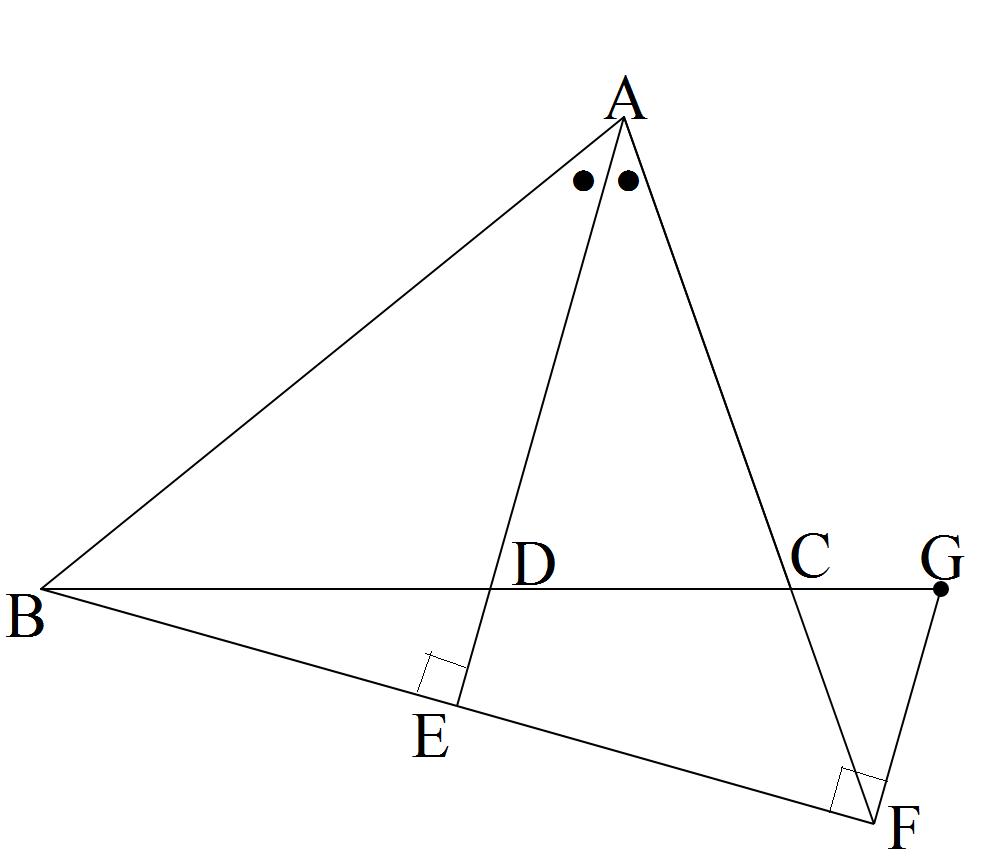
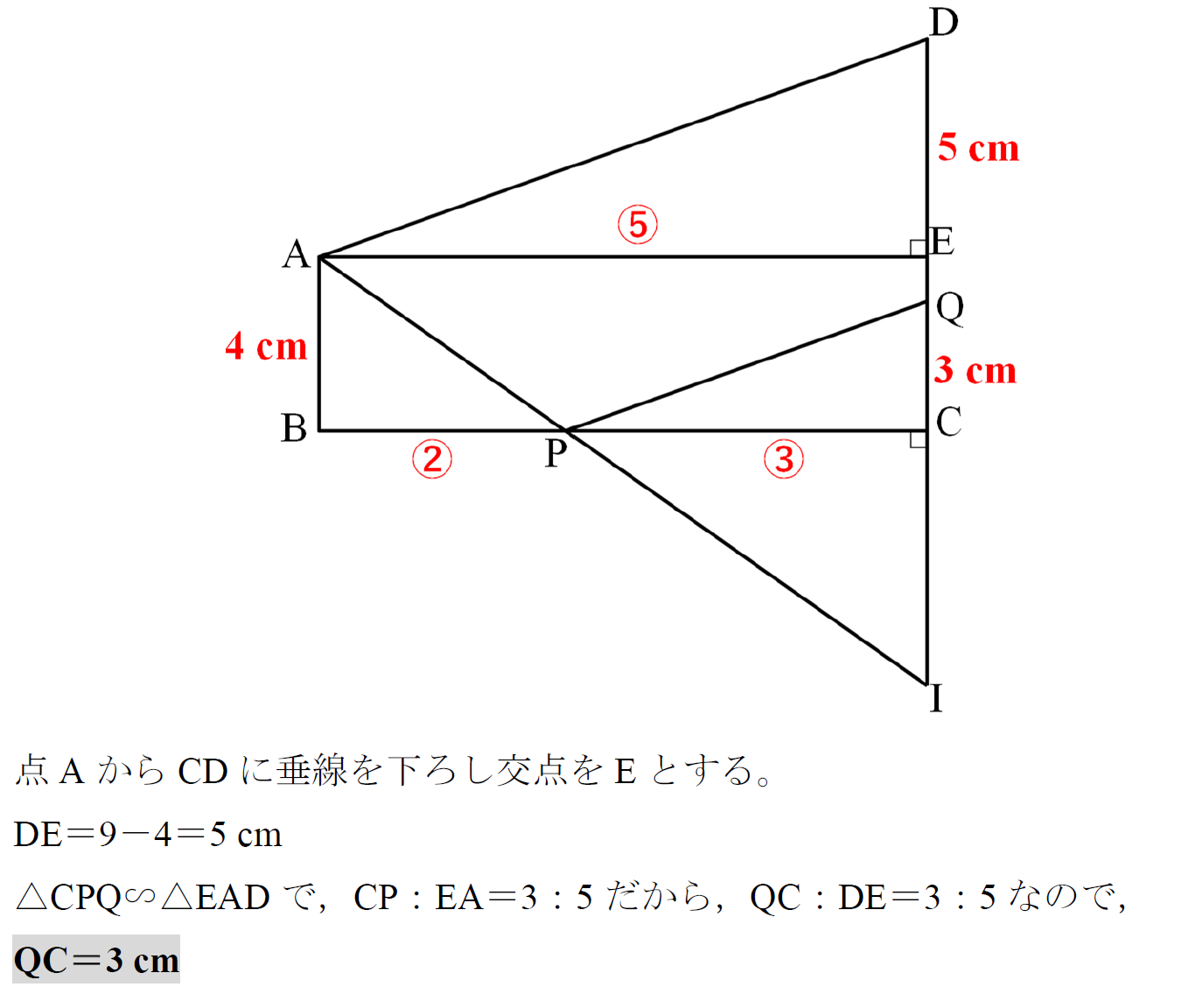
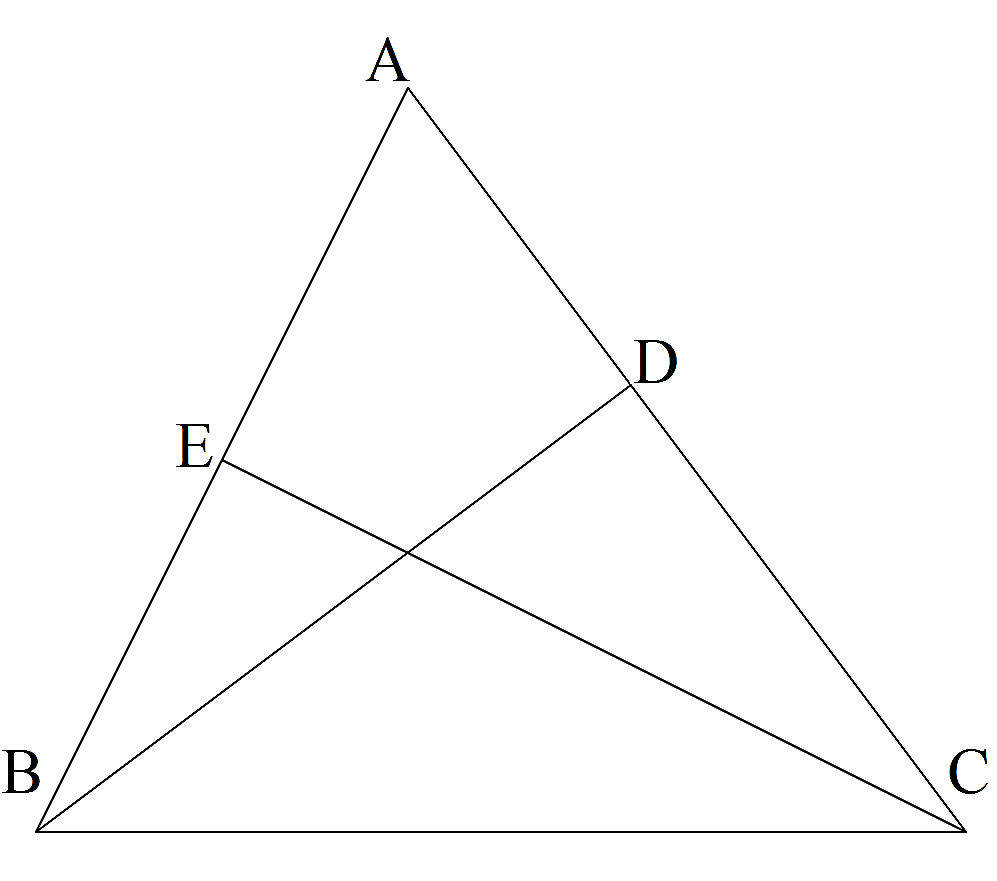
　下の図のようにAB＝3，AC＝2の△ABCがあります。∠Aの二等分線と辺BCとの交点をDとします。直線AD上に，∠AEB＝90°となるように，点Eをとります。次の問いに答えなさい。

問1　AD：DEを求めなさい。
問2　△ADCと△BDEの面積比を，最も簡単な整数の比で表しなさい。

コメント，解説なども「続きから読む」をクリックお願いします。

» more

（2016年度日比谷高校など）例外最短距離

2019/07/27

カテゴリ：@ 空間図形

Tag: 高校入試中学数学立体図形三平方の定理相似

-スポンサーリンク-

シンプルな図ながら，結構長い計算を要求されます。しかし，答え，計算過程は非常にキレイです。解いていて気持ちよいです。上手くいけば。

芸術的な高校入試第6回
「例外最短距離」
出典：2016年度　都立日比谷高校
難易度：★×5，美しさ：★×5，総試験時間：50分，配点：25点/100点

↓解答解説，PDFなどは続きから

» more

【改】半円における難問証明と等脚台形（2015年立川高校など）

2019/07/26

カテゴリ：@ 平面（証明メイン）

Tag: 高校入試中学数学証明円周角合同

-スポンサーリンク-

シンプルな図ながら，色々な能力が適度に問われます。

証明問題は，様々な解法があります。採点大変そう！

芸術的な高校入試第5回
出典：2015年度　東京都立立川高校など大問3
難易度：★★★★☆☆ 美しさ：★★★★☆☆
総試験時間：50分配点：25点/100点

＜PDF，解答例はこちら↓↓＞

» more

シンプルな図だが補助線（2010年新宿高校）

2019/07/24

カテゴリ：@ 平面（証明メイン）

Tag: 高校入試中学数学証明合同相似

-スポンサーリンク-

※メールフォームで，ご意見をいただいたので，解法を追加しました。
※メールフォームで別解をいただいたので，さらに解法を追加しました。2022/04/03

与えられた図は非常にシンプルですが......?
条件の与え方がわざとらしいことに着目出来れば勝ちです。

芸術的な高校入試第4回
出典：2010年度　東京都立新宿高校大問3
難易度：★★★★★★+　美しさ：★★★★★★+
総試験時間：50分配点：23点/100点

　下の図のように，AB＜DC，∠ABC＝∠BCD＝90°の台形があります。∠BADの二等分線が，線分BCと交わるとき，交点をPとします。次の問いに答えなさい。

問1　AB＋DC＝ADとします。
（1）点Pは辺BCの中点であることを証明しなさい。
（2）AB＝4 cm，DC＝9 cmのとき，線分APの長さを求めなさい。
問2　点Pから辺ADに平行な直線を引き，辺DCとの交点をQとします。
（1）点Qを，定規とコンパスを用いて作図しなさい。ただし，作図に用いた線は消さないでおくこと。
（2）AB＝4 cm，DC＝9 cm，BP：PC＝2：3のとき，線分CQの長さを求めなさい。

＜PDF，解答解説はこちら↓↓＞

» more

【改】図が簡素な長い証明（2016年立川高校など）

2019/07/23

カテゴリ：@ 平面（証明メイン）

Tag: 高校入試中学数学証明円周角相似

-スポンサーリンク-

※2021/01/11　解答例追加

図が簡素な証明ですが......？

今後，このブログでこの図を大量に見ることになると思います。

芸術的な高校入試第3回
出典：2016年度　東京都立立川高校など（グループ作成校）大問3
難易度：★★★★☆☆ 美しさ：★★★★☆☆
総試験時間：50分配点：18点/100点
　下の図のように，鋭角三角形ABCがあります。頂点B，Cからそれぞれ辺AC，ABに垂線を下ろし，交点をそれぞれD，Eとします。次の問いに答えなさい。

問1　△ABC∽△ADEを証明しなさい。
問2　AB＝13 cm，AC＝14 cm，BC＝15 cmとします。線分DEの長さを求めなさい。

【解答，コメント等は続きからをクリック↓】

» more

高校受験は道具を使える（2015年度北海道）

2019/07/23

カテゴリ：@ 確率

Tag: 中学数学高校入試数学関数確率

-スポンサーリンク-

2024/02/12　見やすく修正＆解説追加

高校入試という箱舟の中でしか作られない問題です。
超良い問題です，頭を固くしないように。印刷すると良いですね。実際に手を動かしましょう。

「高校受験は道具を使える」
出典：2015年度　北海道　高校入試　過去問
範囲：関数や確率，難易度：測定不能，美しさ：★×6