-スポンサーリンク-
※メールフォームで，ご意見をいただいたので，解法を追加しました。
※メールフォームで別解をいただいたので，さらに解法を追加しました。2022/04/03
与えられた図は非常にシンプルですが......?
条件の与え方がわざとらしいことに着目出来れば勝ちです。
芸術的な高校入試第4回
出典：2010年度 東京都立 新宿高校 大問3
難易度：★★★★★★+ 美しさ：★★★★★★+
総試験時間：50分 配点：23点/100点
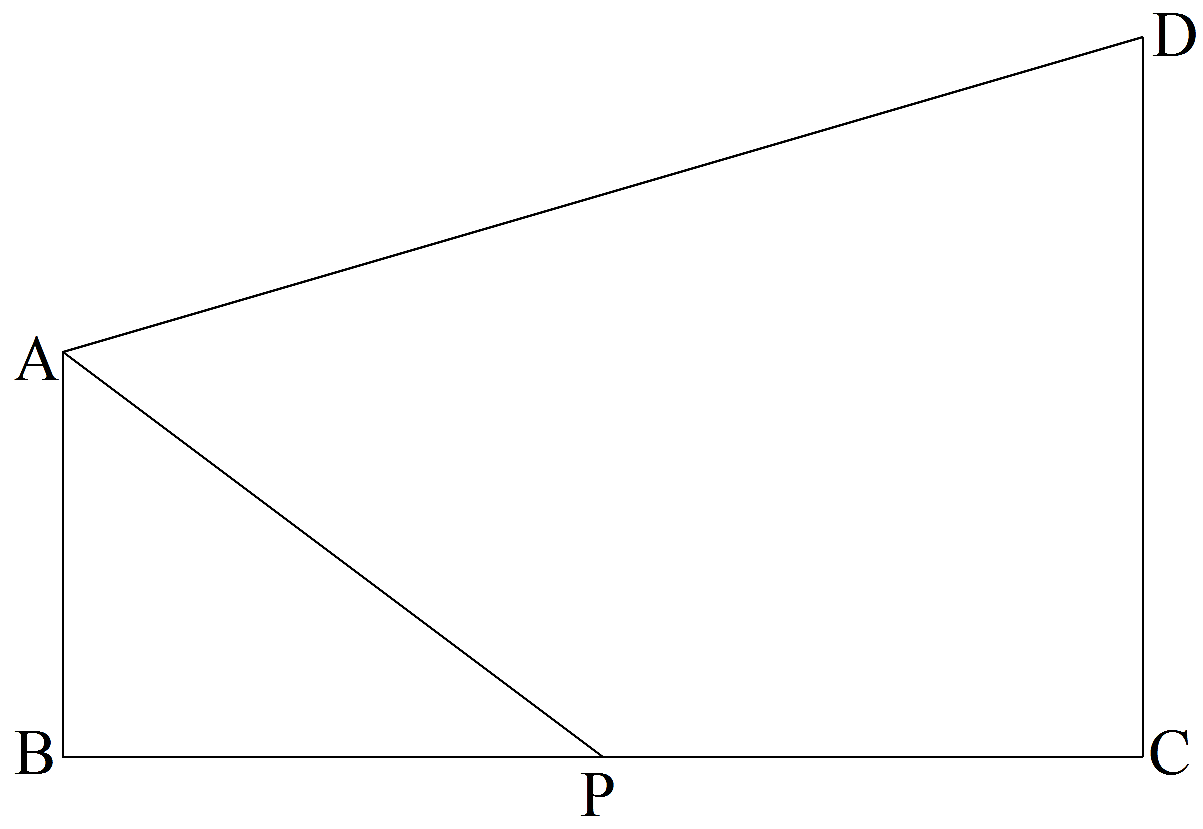
下の図のように，AB＜DC，∠ABC＝∠BCD＝90°の台形があります。∠BADの二等分線が，線分BCと交わるとき，交点をPとします。次の問いに答えなさい。
問1 AB＋DC＝ADとします。
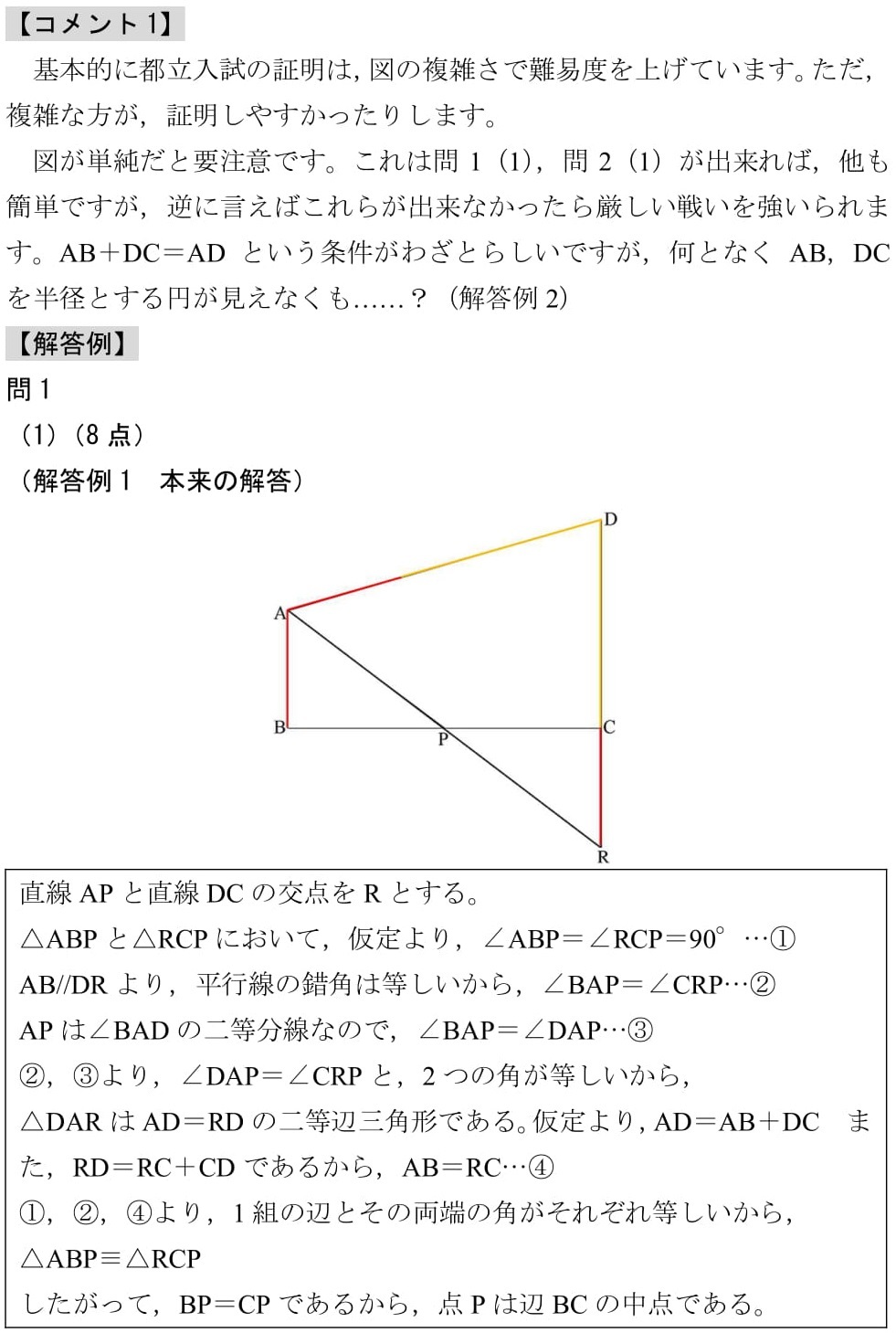
（1）点Pは辺BCの中点であることを証明しなさい。
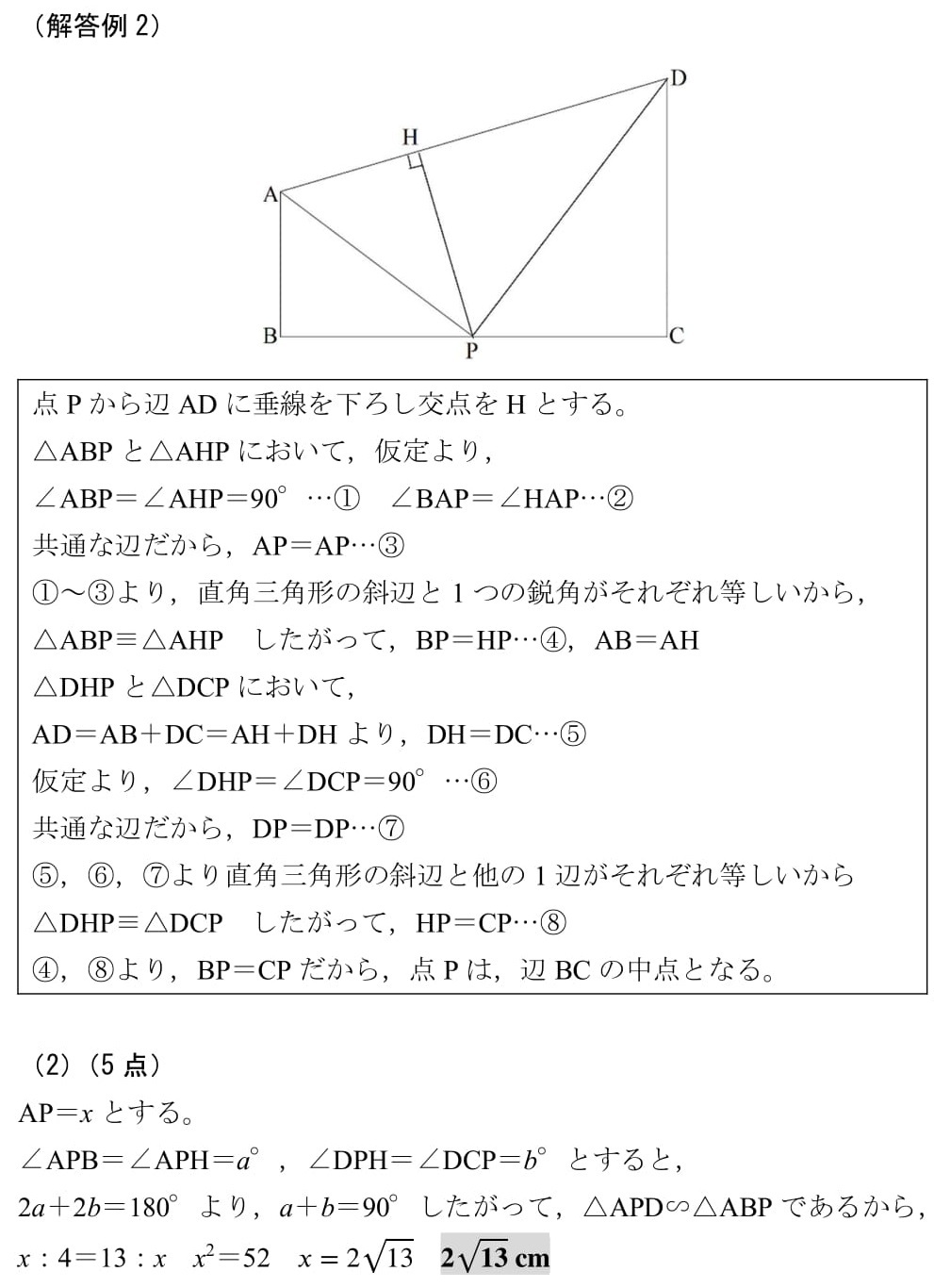
（2）AB＝4 cm，DC＝9 cmのとき，線分APの長さを求めなさい。
問2 点Pから辺ADに平行な直線を引き，辺DCとの交点をQとします。
（1）点Qを，定規とコンパスを用いて作図しなさい。ただし，作図に用いた線は消さないでおくこと。
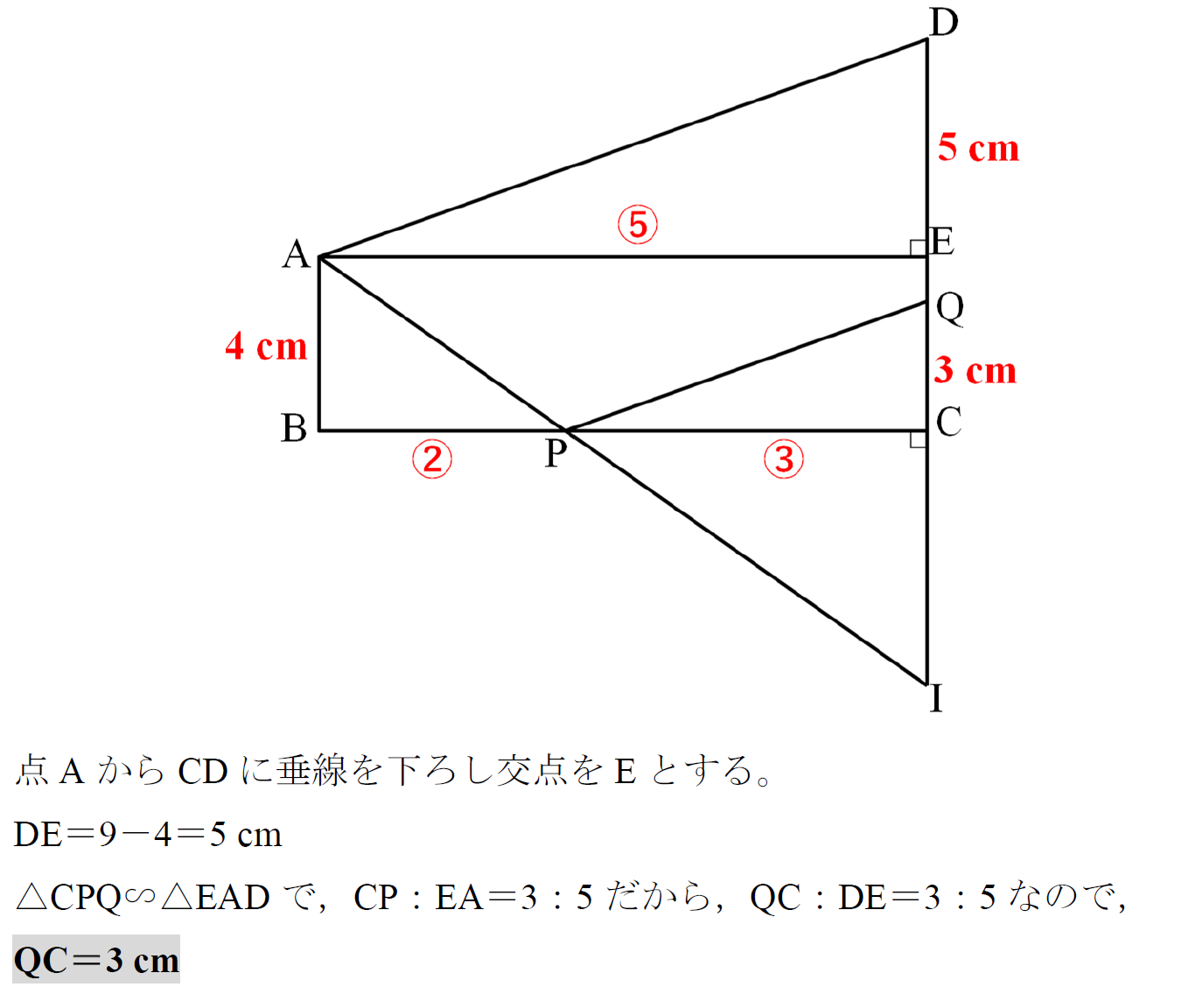
（2）AB＝4 cm，DC＝9 cm，BP：PC＝2：3のとき，線分CQの長さを求めなさい。
＜PDF，解答解説はこちら↓↓＞
※メールフォームで別解をいただいたので，さらに解法を追加しました。2022/04/03
与えられた図は非常にシンプルですが......?
条件の与え方がわざとらしいことに着目出来れば勝ちです。
芸術的な高校入試第4回
出典：2010年度 東京都立 新宿高校 大問3
難易度：★★★★★★+ 美しさ：★★★★★★+
総試験時間：50分 配点：23点/100点
下の図のように，AB＜DC，∠ABC＝∠BCD＝90°の台形があります。∠BADの二等分線が，線分BCと交わるとき，交点をPとします。次の問いに答えなさい。
（1）点Pは辺BCの中点であることを証明しなさい。
（2）AB＝4 cm，DC＝9 cmのとき，線分APの長さを求めなさい。
問2 点Pから辺ADに平行な直線を引き，辺DCとの交点をQとします。
（1）点Qを，定規とコンパスを用いて作図しなさい。ただし，作図に用いた線は消さないでおくこと。
（2）AB＝4 cm，DC＝9 cm，BP：PC＝2：3のとき，線分CQの長さを求めなさい。
＜PDF，解答解説はこちら↓↓＞
PDF
・Seesaaサーバー
別解PDF
※A5サイズです！
＜別解＞
補助線さえしっかり引ければ簡単な問題ですが，中々難しいと思います。0点or23点が多そうです。
嫌らしい難易度の上げ方ですね。
良い問題なので，一度解いておきましょう。
・Seesaaサーバー
別解PDF
※A5サイズです！
＜別解＞
補助線さえしっかり引ければ簡単な問題ですが，中々難しいと思います。0点or23点が多そうです。
嫌らしい難易度の上げ方ですね。
良い問題なので，一度解いておきましょう。
- 関連記事
-
-
受験生大泣き！？真骨頂証明（2010年度北海道）
2020/06/29
-
【改】予想外角の証明？（オリジナル）
2019/04/04
-
（相似難問）い～やそういう条件の与え方があったっていい！（2017年度山口県）
2020/10/20
-
（2021都立西）平行四辺形の難問証明
2021/04/06
-
45（2002年度茨城県改題）（訂正）
2020/10/28
-
理数科な証明(2022年度立川高校)
2022/07/21
-
どの三角形の合同を証明すべきか（2017年度北海道）
2020/07/04
-
【等脚台形】中2，3，高1で解法が異なる証明（オリジナル）【改】
2020/04/28
-
-スポンサーリンク-
comment
> 点Qを求めるとき、並行市変形を作ると考えても良いのではないでしょうか
本当ですね，そちらの方がパターン的でよさそうです。
コメントを送る。