-スポンサーリンク-
※コメントを貰ったので，厳密に解く場合の解法も追加 2022/07/31
私立高校あるある「高校知識前提！？」そんな問題です。どう考えても中線定理を用いるかズルするかしないと（3）は解けません。
兵庫県，私立白陵高校の入試では，高校が発表する模範解答で，高校の確率知識を用いている問題がありました。だからこれも高校知識前提なのか？北海道の私立高校では高校知識前提の問題見たこと......いやたまに光星や第一が出しているか？？
中線定理に関しては，この広島の記事（無理ですね と検索すると何故かTOPにくる記事）でcos使った証明方法載せていましたが，一応中学範囲でも証明可能でしたので，下の方に載せています。
（2）までは公立高校受験の子も解いてみると面白いかもしれません。
「よく分からん問題(中線定理)」
範囲：中3平面図形？ 難易度：★×？
出典：平成23年度 日本大学第二高校
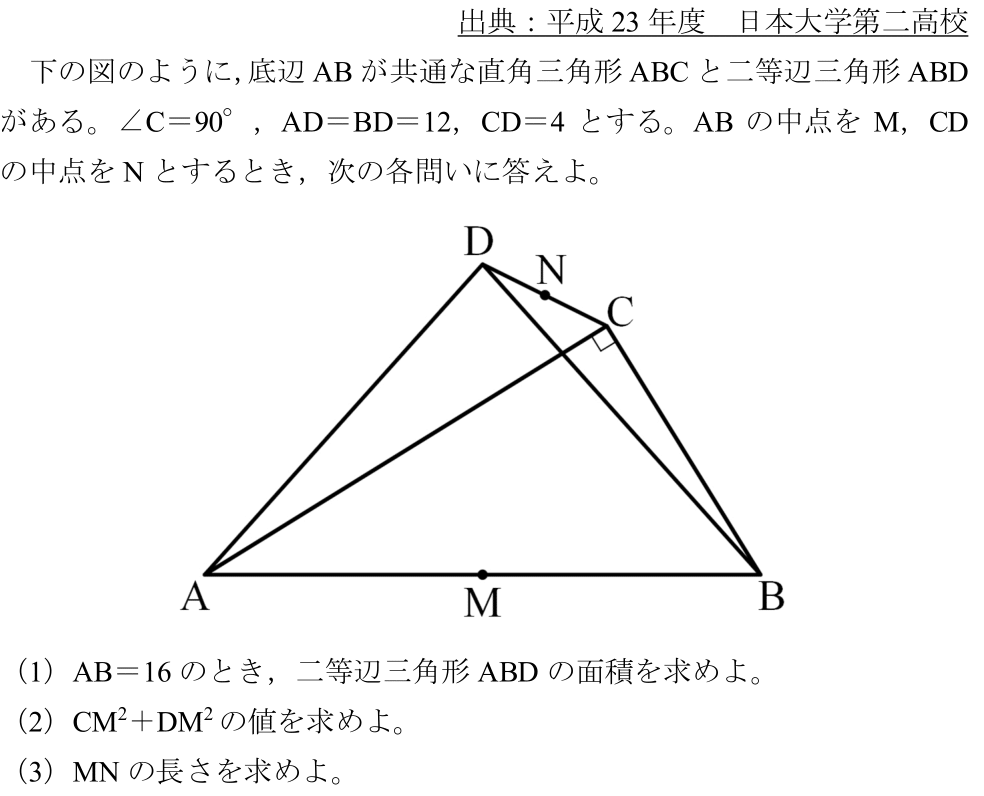
＜問題＞
＜PDF，解答例はこちら↓↓＞
私立高校あるある「高校知識前提！？」そんな問題です。どう考えても中線定理を用いるかズルするかしないと（3）は解けません。
兵庫県，私立白陵高校の入試では，高校が発表する模範解答で，高校の確率知識を用いている問題がありました。だからこれも高校知識前提なのか？北海道の私立高校では高校知識前提の問題見たこと......いやたまに光星や第一が出しているか？？
中線定理に関しては，この広島の記事（無理ですね と検索すると何故かTOPにくる記事）でcos使った証明方法載せていましたが，一応中学範囲でも証明可能でしたので，下の方に載せています。
（2）までは公立高校受験の子も解いてみると面白いかもしれません。
「よく分からん問題(中線定理)」
範囲：中3平面図形？ 難易度：★×？
出典：平成23年度 日本大学第二高校
＜問題＞
＜PDF，解答例はこちら↓↓＞
＜PDF＞※A5サイズです
Audrey2.pdf
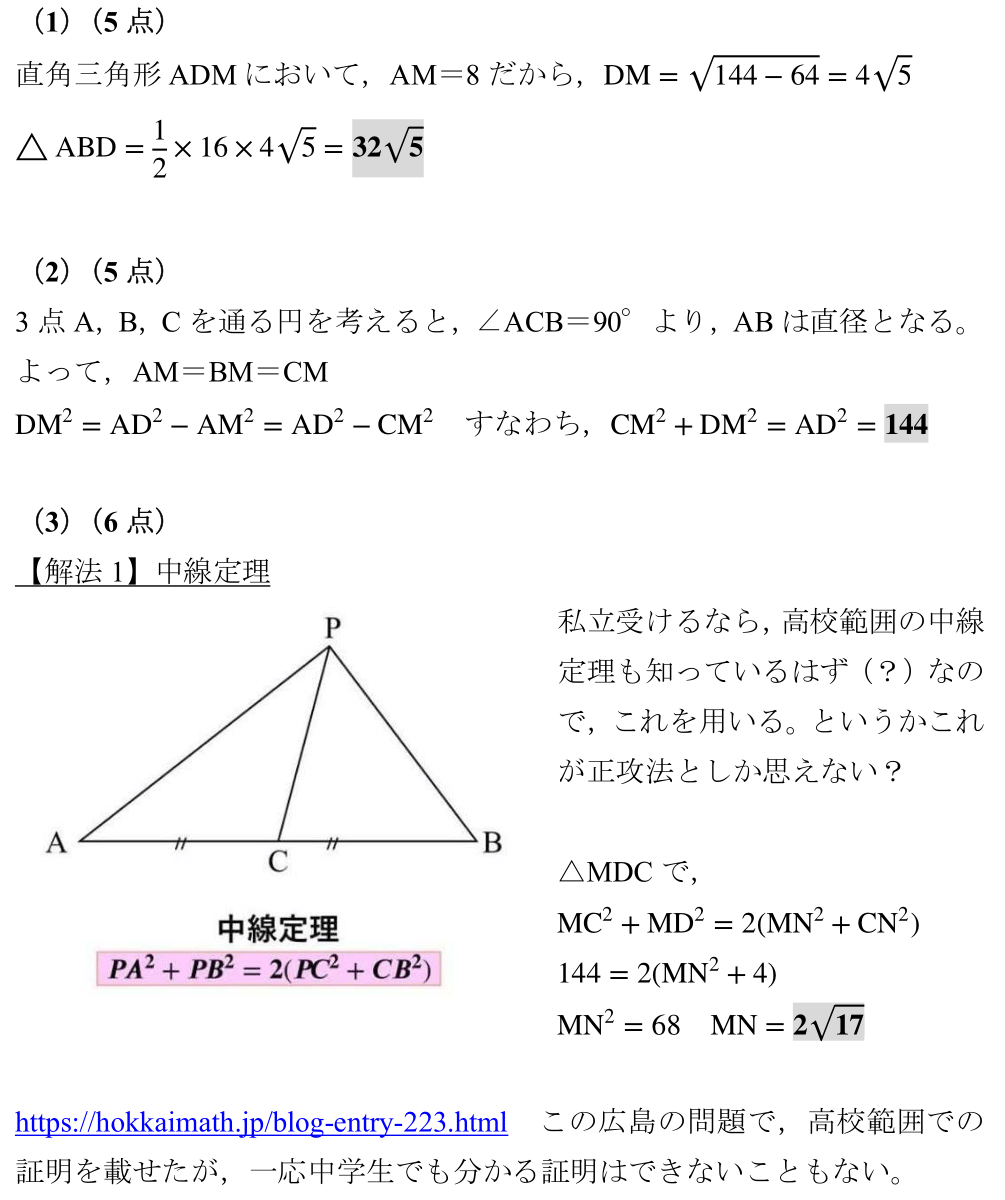
＜解答例＞
中線定理の証明，http://awayajuku.blog81.fc2.com/blog-entry-312.htmlのように座標で表した方が，中学生にも分かりやすいですね，たぶん。
＜厳密に解く場合？ 出題意図？＞
＜コメント＞
中線定理を知らなくても良いし証明しなくても良い，さらに【解法2】のようなズルをしなくても良い解法誰かありましたら，教えてください。私の頭じゃ無理でした。
CM^2+DM^2の誘導が露骨すぎて，中線定理としか思えない……。（2）までは面白い問題です。
～一覧の一覧～
・関数 一覧
・平面図形 一覧
・空間図形 一覧
・その他の問題（確率や整数など） 一覧
・難問一覧（★×5以上）
- 関連記事
-
-
ベクトルの誘惑(2014年度巣鴨高校)
2023/04/23
-
（2021年度愛媛県）ももとモグライダー（折り曲げ長方形）（別解追加）
2021/12/03
-
出典不明の良問
2022/11/19
-
（2021年度京都府）60（適度に差がつく問題）
2021/11/30
-
平面図形と座標設定2(2019日大第一)（別解追加）
2022/01/11
-
(2022年度青学)言うとしたら僕【真空ジェシカ】
2022/12/13
-
分割面積の典型難問（2005年宮城改題）
2020/12/28
-
中2で解ける線分・面積比問題（2021広島県大問3）
2021/06/16
-
-スポンサーリンク-
comment
こんにちは。Muglythと申します。2014年に高校受験をした身で、数学が好きで受験生時代には色んな高校の入試問題を手あたり次第解いていたのですが、こんな問題があったとは知らず興味深く読ませていただきました。
私なりに出題者の想定解法および出題意図を考えてみました。5カ月も前の記事ですので既出でしたら申し訳ありません。
MからCDに降ろした垂線の足をHとし、ＭＮ＝x、NH＝yとおく。
すると三角形ＭＮＨにおいて、三平方の定理より
MH^2 + y^2 = x^2 ・・・⓵
ここで、「Hが線分ＣＮ上にあるとする」と三角形ＭＣＨと三角形ＭＤＨにおいて
MH^2 + (2 - y)^2 =MC^2 ・・・②
MH^2 + (2 + y)^2 = MD^2 ・・・③
②と③の辺々足して
2MH^2 + 2y^2 + 4 = MC^2 + MD^2 ・・・④
④から⓵の辺々を2倍したものを引くと
4 ＝ MC^2 + MD^2 -x^2 ・・・⑤
つまりx^2 = 140
⑤で結果的に出てくる式は中線定理そのものですが、MC^2 + MD^2 を求めよという問題を作れそうな図形を出してきたうえで(2)でわざわざMC^2 + MD^2 を求めさせていることから推察するに、
「Ｈの位置関係が分からないから ②で(2 - y)が(y-2)に変わったりするけど、どうせ2乗するから値としては変わらないよね。それに場合分けによっては②や③の式でＭＣとＭＤが入れ替わったりもするけど、（(2)で求めたMC^2 + MD^2を使える形を作り出すために）②と③の２式を足し合わせてみたら煩雑な場合分けをひとまとめに考えられたことになるってことに気付いてね」という出題者からのパズル的挑戦だったのではないでしょうか。
（そして回答者はyを消去するために式を足し引きするパズルをしているだけの感覚なので自分が中線定理を導出していることに気付かない）
出題意図はそうかもしれませんね。解答例では場合分けしていますが，Hの位置がどうであろうが（Hが線分CD上にあろうが外にあろうが），結局足し合わせると同じですね。
ただ，4点M，C，D,Nが同一直線上にある場合はその解き方できない（結局中線定理は成り立つのですが），私としては，そのような出題意図だったとしたらちょっと嫌ですね。
どちらにせよ，中線定理を知っているか知らないかで差がつきすぎるので，あまり好きな問題ではありません。
> こんにちは。Muglythと申します。2014年に高校受験をした身で、数学が好きで受験生時代には色んな高校の入試問題を手あたり次第解いていたのですが、こんな問題があったとは知らず興味深く読ませていただきました。
> 私なりに出題者の想定解法および出題意図を考えてみました。5カ月も前の記事ですので既出でしたら申し訳ありません。
>
> MからCDに降ろした垂線の足をHとし、ＭＮ＝x、NH＝yとおく。
> すると三角形ＭＮＨにおいて、三平方の定理より
> MH^2 + y^2 = x^2 ・・・⓵
> ここで、「Hが線分ＣＮ上にあるとする」と三角形ＭＣＨと三角形ＭＤＨにおいて
> MH^2 + (2 - y)^2 =MC^2 ・・・②
> MH^2 + (2 + y)^2 = MD^2 ・・・③
> ②と③の辺々足して
> 2MH^2 + 2y^2 + 4 = MC^2 + MD^2 ・・・④
> ④から⓵の辺々を2倍したものを引くと
> 4 ＝ MC^2 + MD^2 -x^2 ・・・⑤
> つまりx^2 = 140
>
> ⑤で結果的に出てくる式は中線定理そのものですが、MC^2 + MD^2 を求めよという問題を作れそうな図形を出してきたうえで(2)でわざわざMC^2 + MD^2 を求めさせていることから推察するに、
> 「Ｈの位置関係が分からないから ②で(2 - y)が(y-2)に変わったりするけど、どうせ2乗するから値としては変わらないよね。それに場合分けによっては②や③の式でＭＣとＭＤが入れ替わったりもするけど、（(2)で求めたMC^2 + MD^2を使える形を作り出すために）②と③の２式を足し合わせてみたら煩雑な場合分けをひとまとめに考えられたことになるってことに気付いてね」という出題者からのパズル的挑戦だったのではないでしょうか。
>
> （そして回答者はyを消去するために式を足し引きするパズルをしているだけの感覚なので自分が中線定理を導出していることに気付かない）
コメントを送る。