-スポンサーリンク-
※問3（1） 解答例 （誤）x=6 （正）x=√6
2016年度は，難易度が若干ぶり返した......わけではないのですが，難易度見極めできなかった受験生が多く，難しい年となってしまいました。
難易度見極めの練習として，2016年度はちょうどよいでしょう。
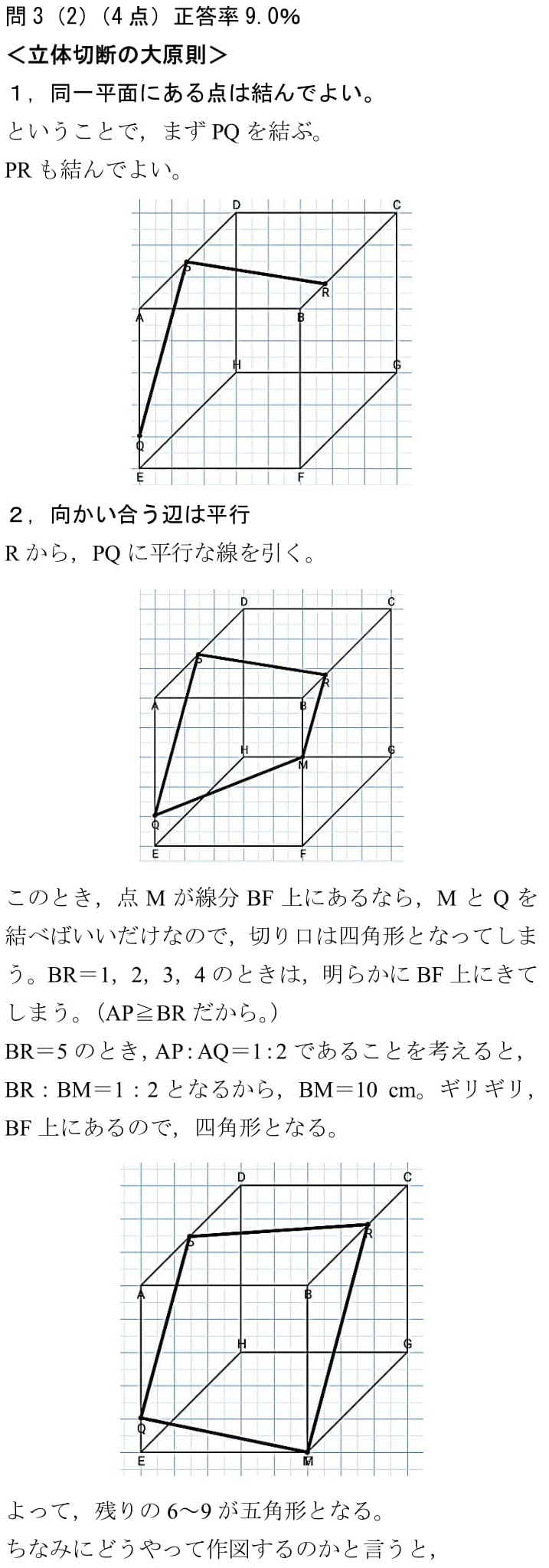
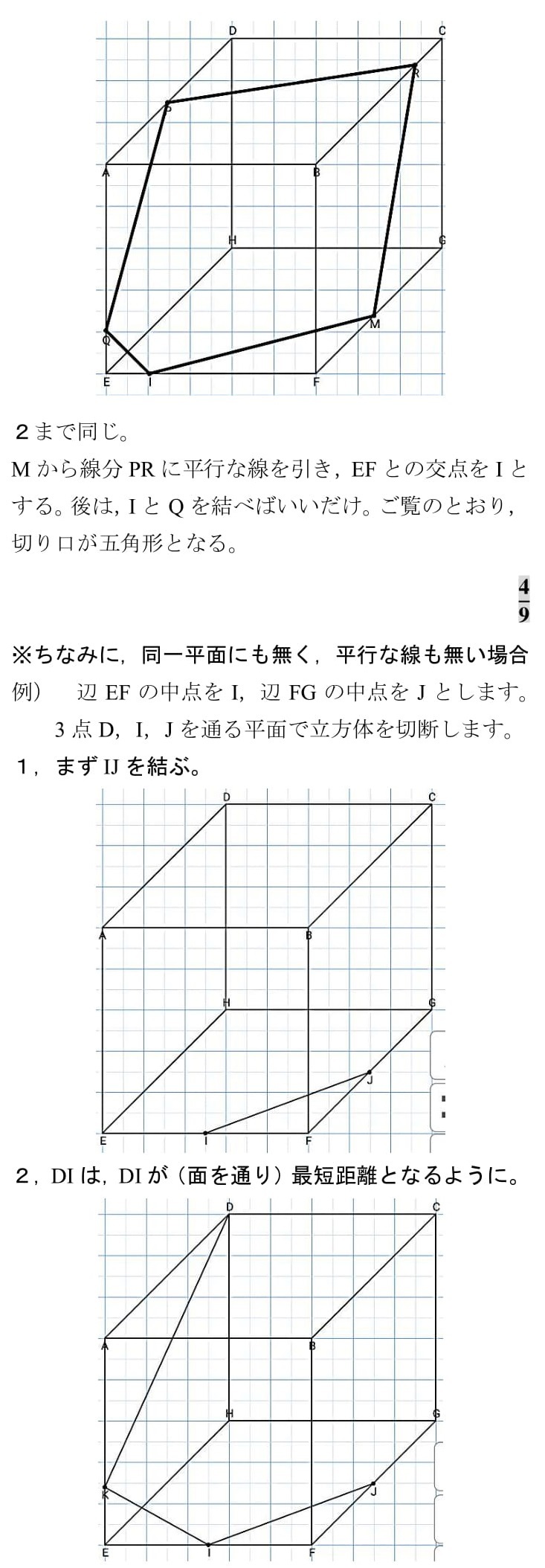
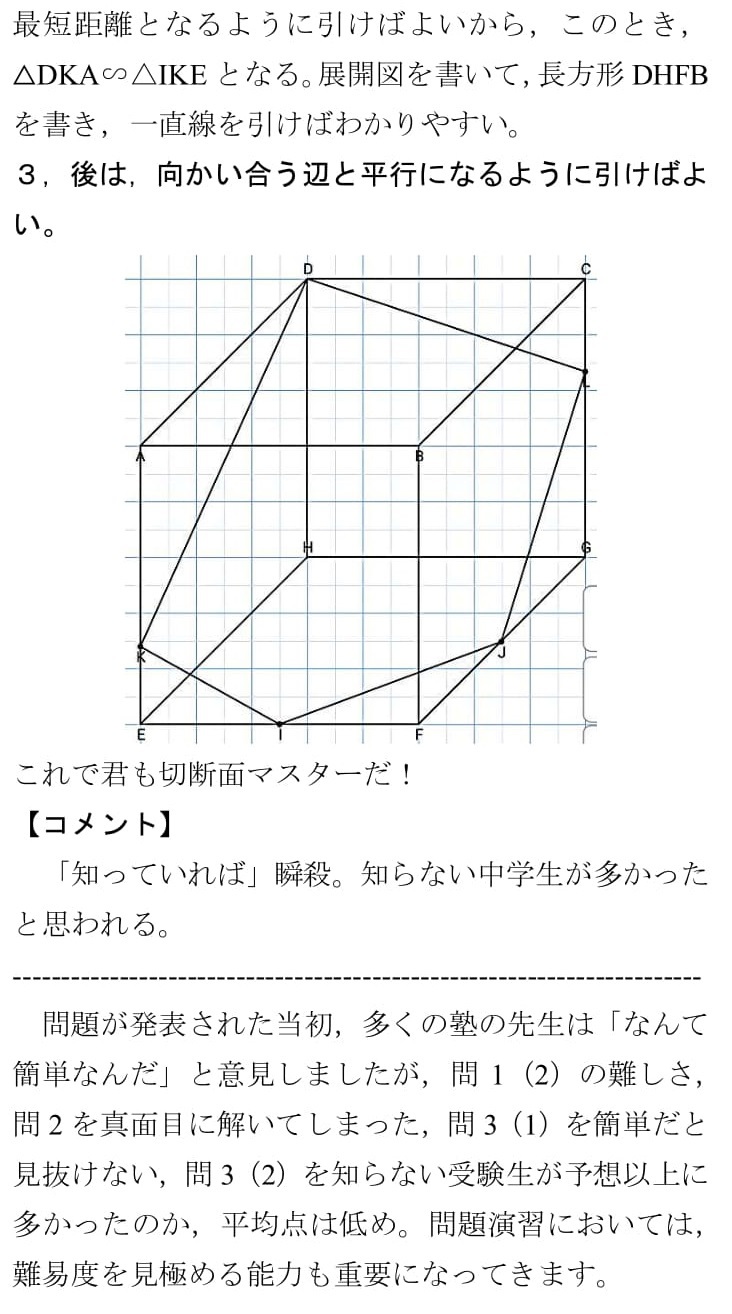
立方体切断の話が出ています。知っていれば瞬殺，知らなければOUTです。知らない受験生の方が多かったので，プリント内で詳しく解説しておきました。「向かい合う辺は平行！」これさえ知っていればなんとかなります。
2016年度 裁量問題 数学 解説
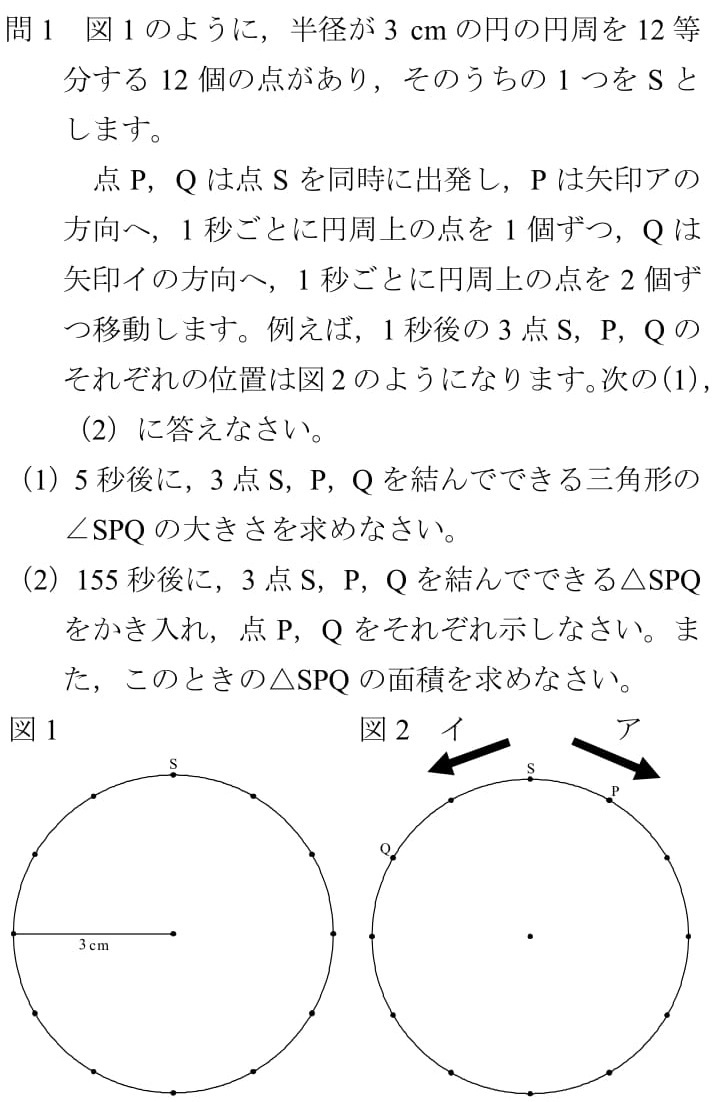
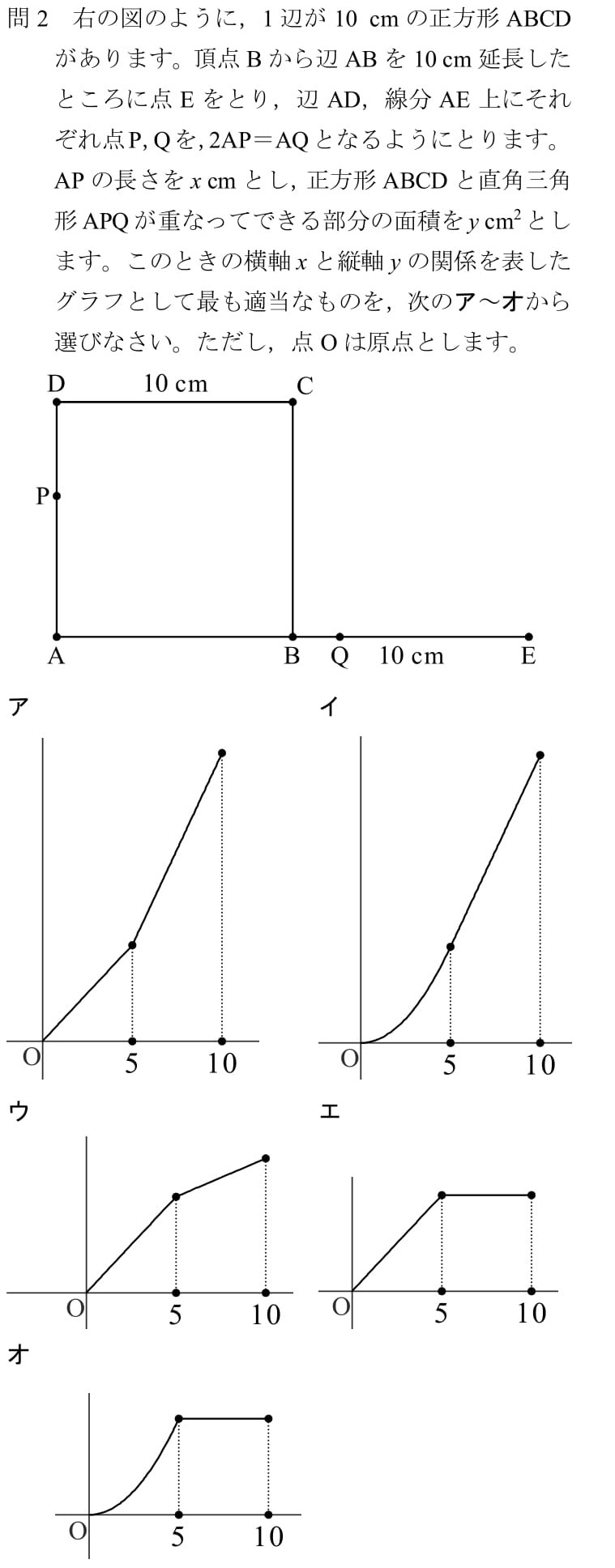
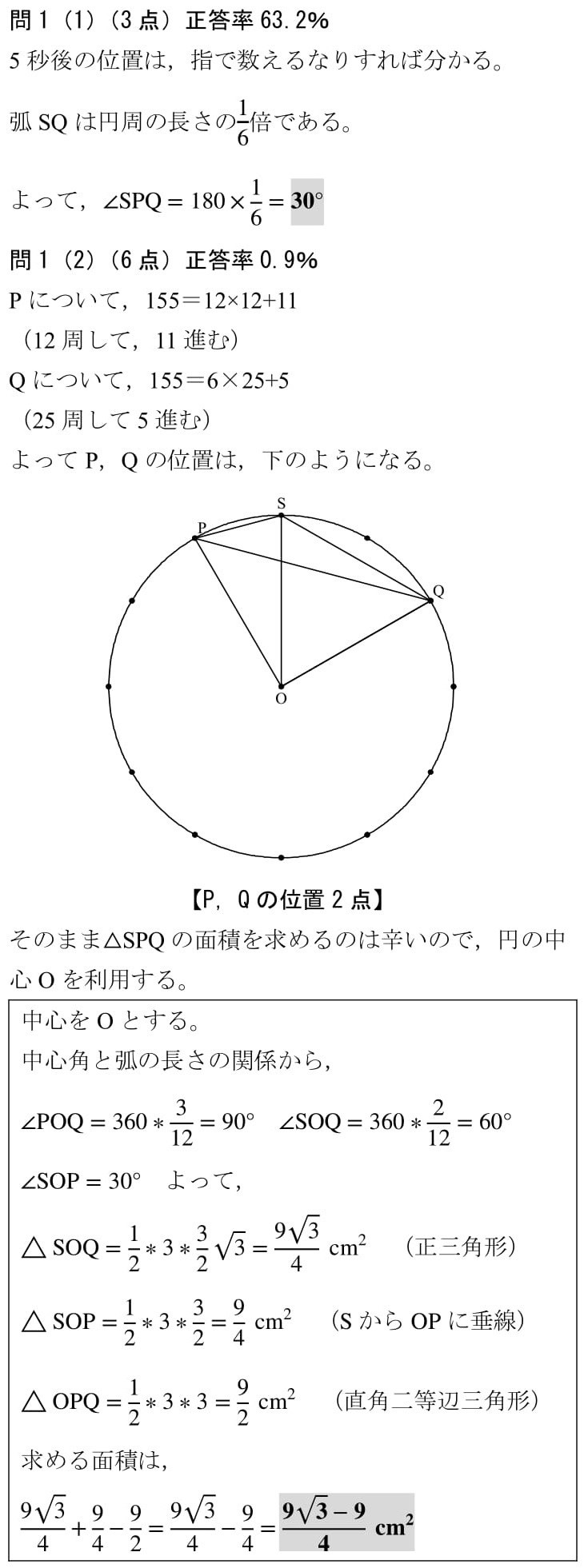
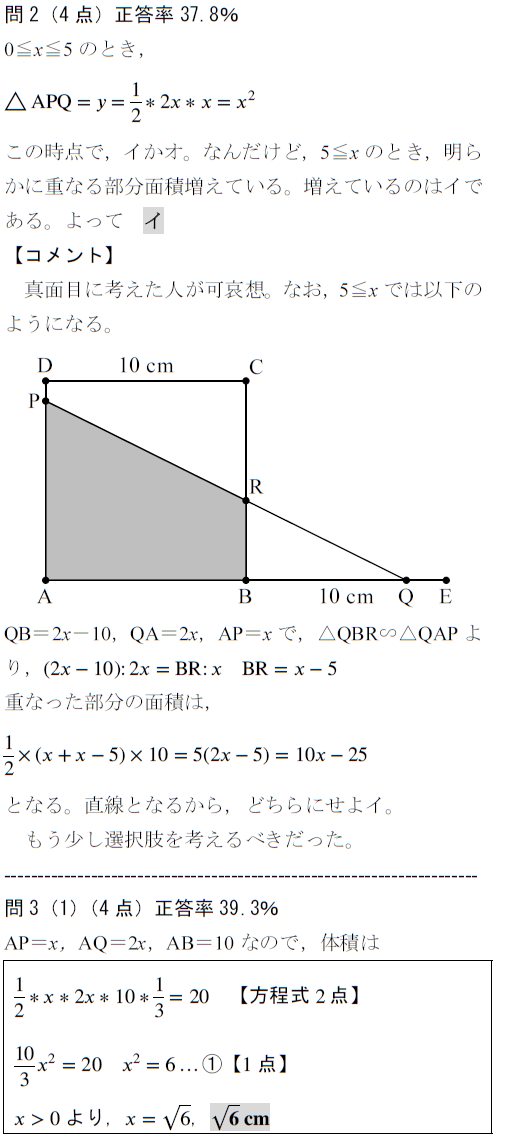
出題分野：平面図形，規則性，関数，確率，立体切断
出典：平成28年度 北海道 公立高校入試 過去問
URL：http://www.koukou.hokkaido-c.ed.jp/gakuryokukensa/h31gakuryoku.html
＜問題＞
＜解答解説，PDFはこちら↓↓＞
2016年度は，難易度が若干ぶり返した......わけではないのですが，難易度見極めできなかった受験生が多く，難しい年となってしまいました。
難易度見極めの練習として，2016年度はちょうどよいでしょう。
立方体切断の話が出ています。知っていれば瞬殺，知らなければOUTです。知らない受験生の方が多かったので，プリント内で詳しく解説しておきました。「向かい合う辺は平行！」これさえ知っていればなんとかなります。
2016年度 裁量問題 数学 解説
出題分野：平面図形，規則性，関数，確率，立体切断
出典：平成28年度 北海道 公立高校入試 過去問
URL：http://www.koukou.hokkaido-c.ed.jp/gakuryokukensa/h31gakuryoku.html
＜問題＞
＜解答解説，PDFはこちら↓↓＞
＜PDF＞
Sairyo_math_2016_2.pdf
＜解答・解説＞
立方体切断について覚えておくとともに，自分はどのような問題を解くべきなのか考えてみましょう。
Sairyo_math_2016_2.pdf
＜解答・解説＞
立方体切断について覚えておくとともに，自分はどのような問題を解くべきなのか考えてみましょう。
- 関連記事
-
-
(2022日比谷)代入パズル空間図形
2022/02/24
-
【正答率0.7%】(2017年度大阪府C)有能な誘導(ついでにキングオブコント2022感想)
2022/10/08
-
(2022年度開成)正多面体X
2022/05/22
-
見取り図(2014年度東京学芸大学附属高校)
2023/02/10
-
最後の一撃は、せつない。(2023年度国立高校)
2023/05/24
-
中1空間図形の知識だけで解ける？（2018年度立川高校）
2020/08/23
-
(2023年度灘高校)立方体切断の難問
2023/02/22
-
（2011渋幕）立体を平面図で，正四面体を切り分ける（高校受験）
2021/09/27
-
-スポンサーリンク-
comment
x^2=6なので、x=±√6,x＞0より、x=√6 では?
コメントを送る。