-スポンサーリンク-
※2021年10/15に訂正
あけおめです。
新年早々，異常に難しい問題をご紹介します。2018年度日比谷高校の過去問を元に作成しました。
問1はオリジナル，問2は日比谷の問題を少しアレンジ。いかに立体を平面で考えるかが重要です。
こんなに難しい問題は，北海道では100％出ませんね。
「正六角柱と容赦ない計算」
出典：平成30年度 日比谷高校 と オリジナル
範囲：空間図形，三平方の定理 難易度：★★★★★++
＜問題＞
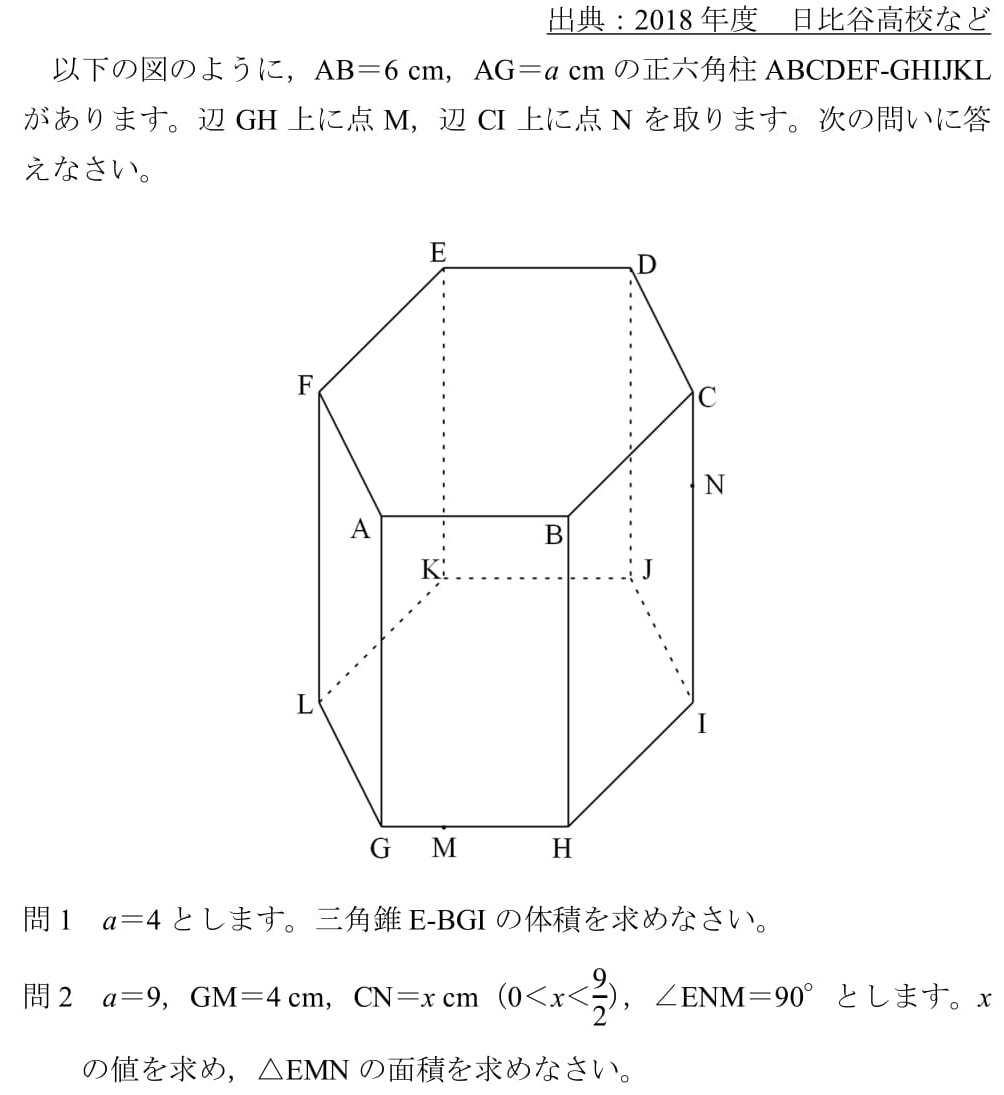
＜PDF,解答例はこちら↓↓＞
あけおめです。
新年早々，異常に難しい問題をご紹介します。2018年度日比谷高校の過去問を元に作成しました。
問1はオリジナル，問2は日比谷の問題を少しアレンジ。いかに立体を平面で考えるかが重要です。
こんなに難しい問題は，北海道では100％出ませんね。
「正六角柱と容赦ない計算」
出典：平成30年度 日比谷高校 と オリジナル
範囲：空間図形，三平方の定理 難易度：★★★★★++
＜問題＞
＜PDF,解答例はこちら↓↓＞
＜PDF＞※A5サイズです
・Seesaaサーバー
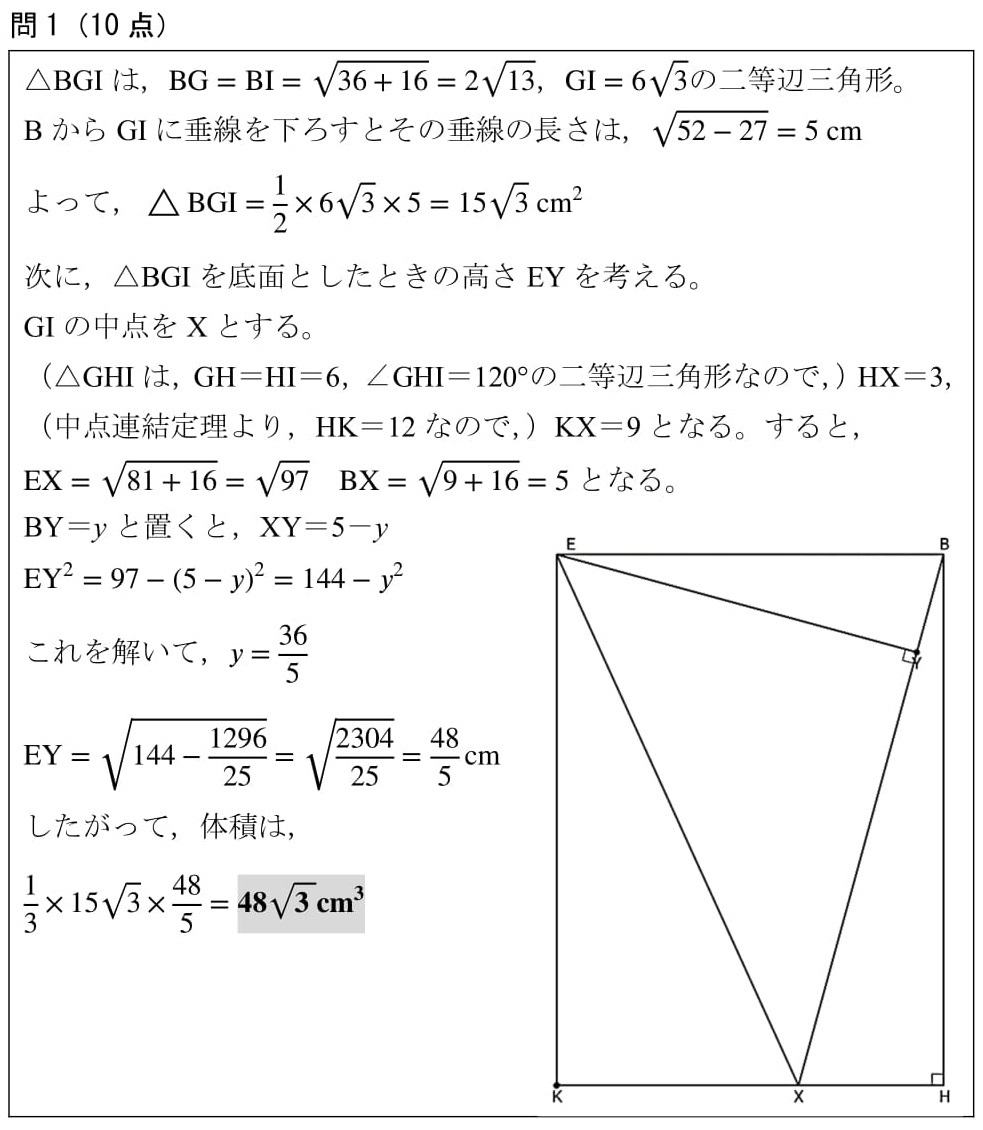
＜解答例＞
＜コメント＞
問1はオリジナル，問2は日比谷の問題です。都立独自校という，その名の通り特殊な入試対応用です。
ただ，独自校は，解答が長くなるだけで，必要な知識1個1個は難しくありません。いかに長く思考できるかです。それが難しいのだけどね。
日比谷と，北海道の札幌南は，同じ公立同士だからか？よくセンター試験の平均点で競い合ったり，授業見学をしたりしているらしいです。確かにどちらも公立TOPだけど，日比谷は周りに東京開成だの，有名私立ある中で，生徒募集で戦っていますからね。どう考えても南の方が有利？（札幌は南以外のTOP高校と言ったら，北と北嶺ぐらい？）
～一覧の一覧～
・関数 一覧
・平面図形 一覧
・空間図形 一覧
・その他の問題（確率や整数など） 一覧
・Seesaaサーバー
＜解答例＞
＜コメント＞
問1はオリジナル，問2は日比谷の問題です。都立独自校という，その名の通り特殊な入試対応用です。
ただ，独自校は，解答が長くなるだけで，必要な知識1個1個は難しくありません。いかに長く思考できるかです。それが難しいのだけどね。
日比谷と，北海道の札幌南は，同じ公立同士だからか？よくセンター試験の平均点で競い合ったり，授業見学をしたりしているらしいです。確かにどちらも公立TOPだけど，日比谷は周りに東京開成だの，有名私立ある中で，生徒募集で戦っていますからね。どう考えても南の方が有利？（札幌は南以外のTOP高校と言ったら，北と北嶺ぐらい？）
～一覧の一覧～
・関数 一覧
・平面図形 一覧
・空間図形 一覧
・その他の問題（確率や整数など） 一覧
- 関連記事
-
-
（2018年日比谷高校）正六角柱と容赦ない計算（訂正済）
2020/01/01
-
(2022年度開成)正多面体X
2022/05/22
-
よく見る空間図形かと思いきや(2023年度函館ラ・サール高校)
2023/11/15
-
(2003年度北海道)ひてぃにき（分割空間図形と記述）オズワルド畠中さんと函館，北斗
2021/12/11
-
正四面体の体積と比率
2019/08/25
-
立体の交点(1980年私立武蔵)
2020/12/07
-
2通りで表す問題の典型例（2017年度茨城県）
2019/08/28
-
ポンデリング空間図形（2017年度熊本県）
2020/12/31
-
-スポンサーリンク-
comment
追記できるかどうかまだ分かりませんが、検証できたらしてみようと思います。
※メアド入力されていたので管理人の方でコメント打ち直しました。
コメントを送る。